Modification - Sentinel Nodes
Consider the push_front()/pop_front() example we did early. Both functions required us to check for a special case and essentially write 2 different versions of the same function for those special cases (inserting into an empty list, removing from a list with only one node). One modification we can make to our linked list in order to simplify the functions is to add the idea of sentinel nodes.
Sentinel nodes are nodes that exist at the front and back of a linked list. These nodes always exist from the time the linked list is created to the time it is destroyed. They do not hold any data. The purpose for their existence is to eliminate most of the special cases when writing functions.
Most of the special cases in our implementations involve checking whether the front_/back_ pointers or next_/prev_ pointers are nullptr/None at the time or not. Sentinel nodes can help us dealing with these situations more easily by preventing these from happening, and let us have our code more simplified. In this section we will look at what it means to have sentinel nodes.
Linked List Constructor - With Sentinels
The constructor of the linked list should set up an empty linked list. With sentinels, this effectively means we create two nodes whose data is undefined and point them at each other. One is the front sentinel the other the back sentinel. These nodes do not hold any data. Their purpose is to reduce special cases.
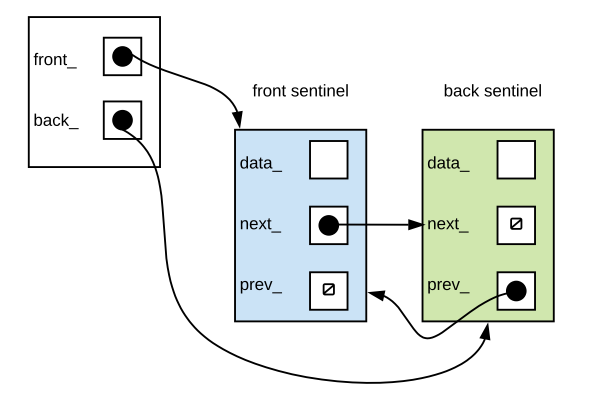
Empty linked lists for linked lists with sentinels will have 2 nodes. The front sentinel and the back sentinel. These are created on list construction.
- Python
- C++
class LinkedList:
class Node:
def __init__(self, data, next=None, prev=None):
self.data = data
self.next = next
self.prev = prev
def __init__(self):
self.front = self.Node(None)
self.back = self.Node(None, None, self.front)
self.front.next = self.back
push_front()
How will push_front change with sentinels?
Step 1: Create new node, next node is the node that follows the front sentinel. The previous node is the front sentinel.
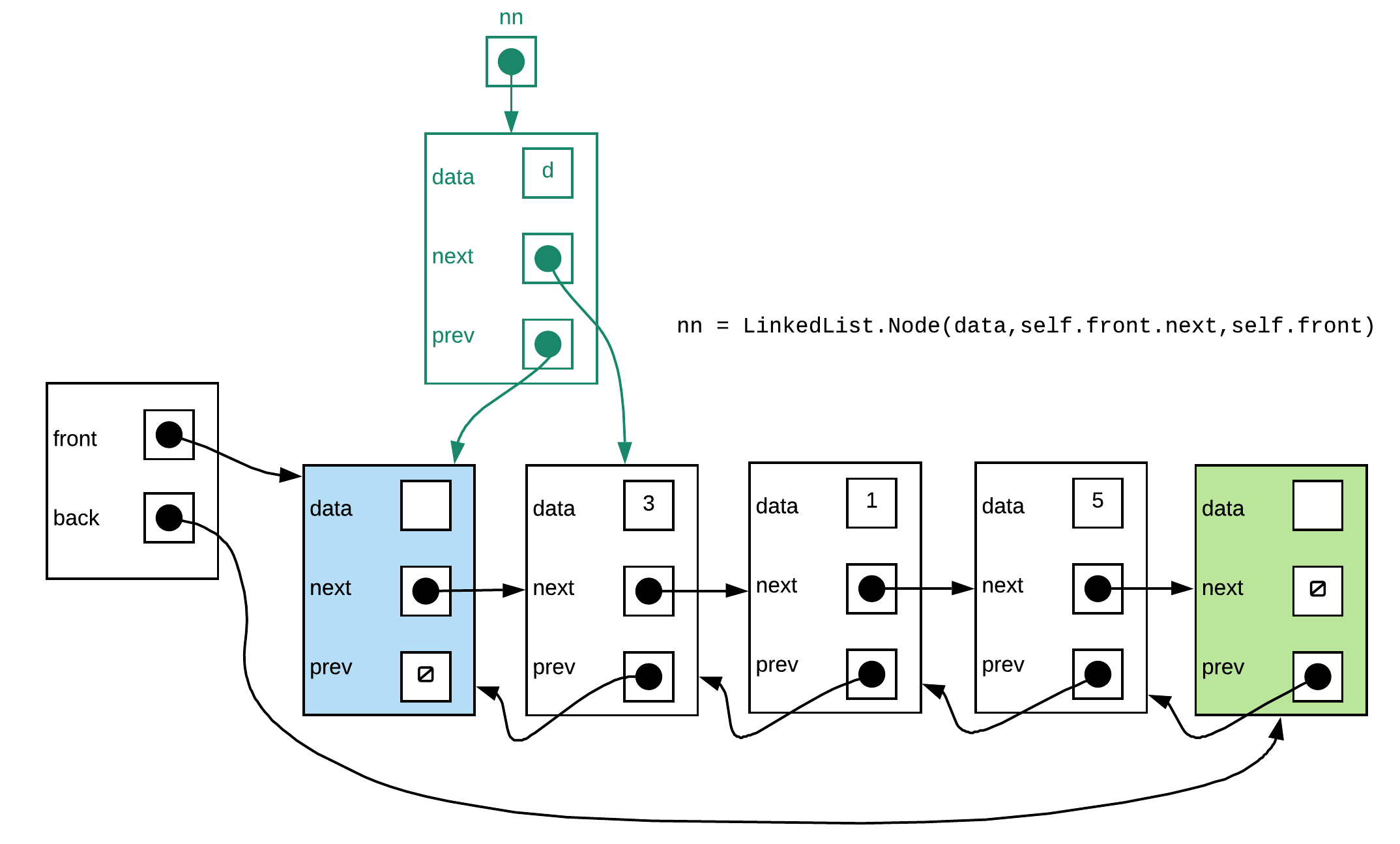
Step 2: Make the previous pointer of the node that follows the front sentinel point to the new node
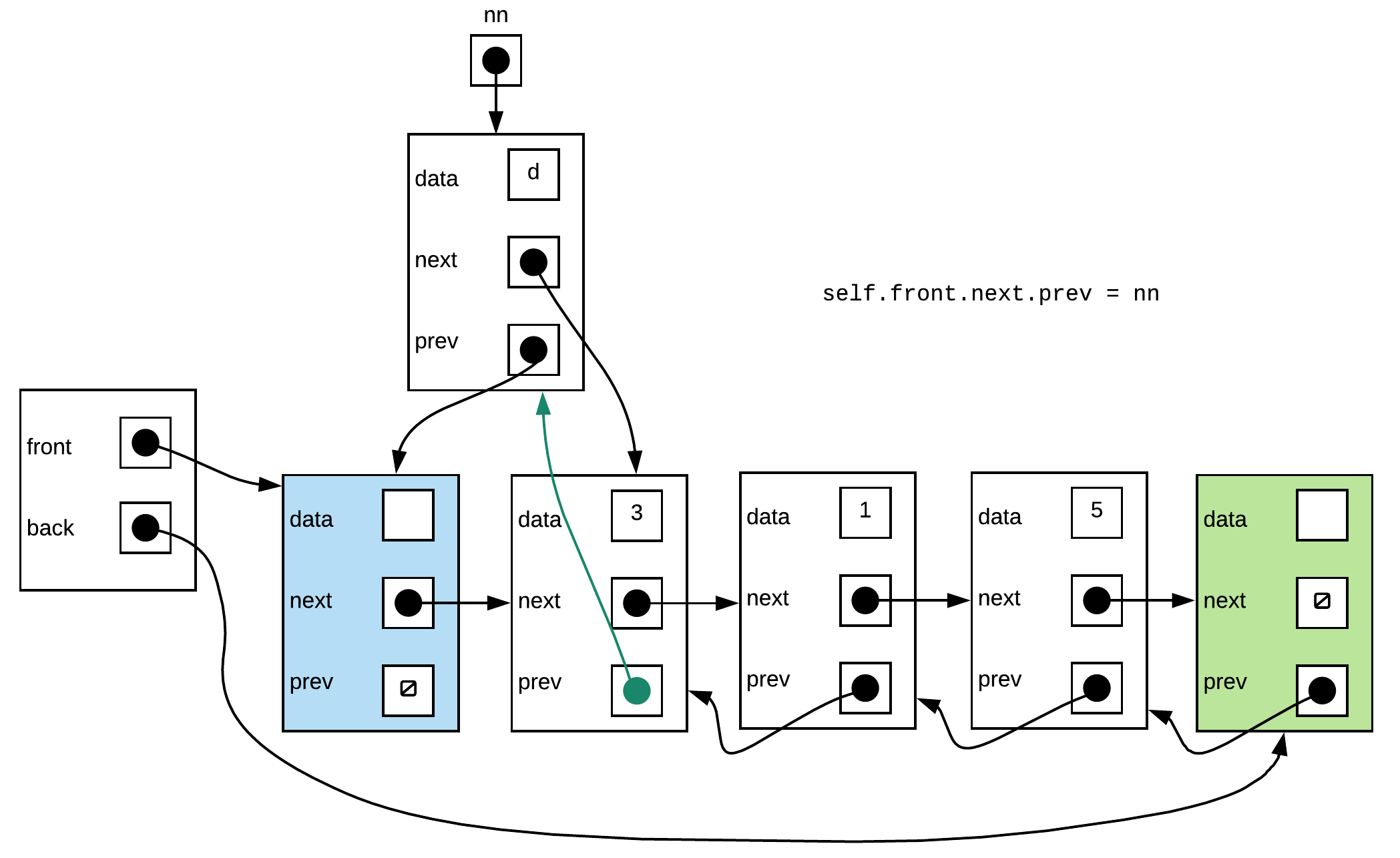
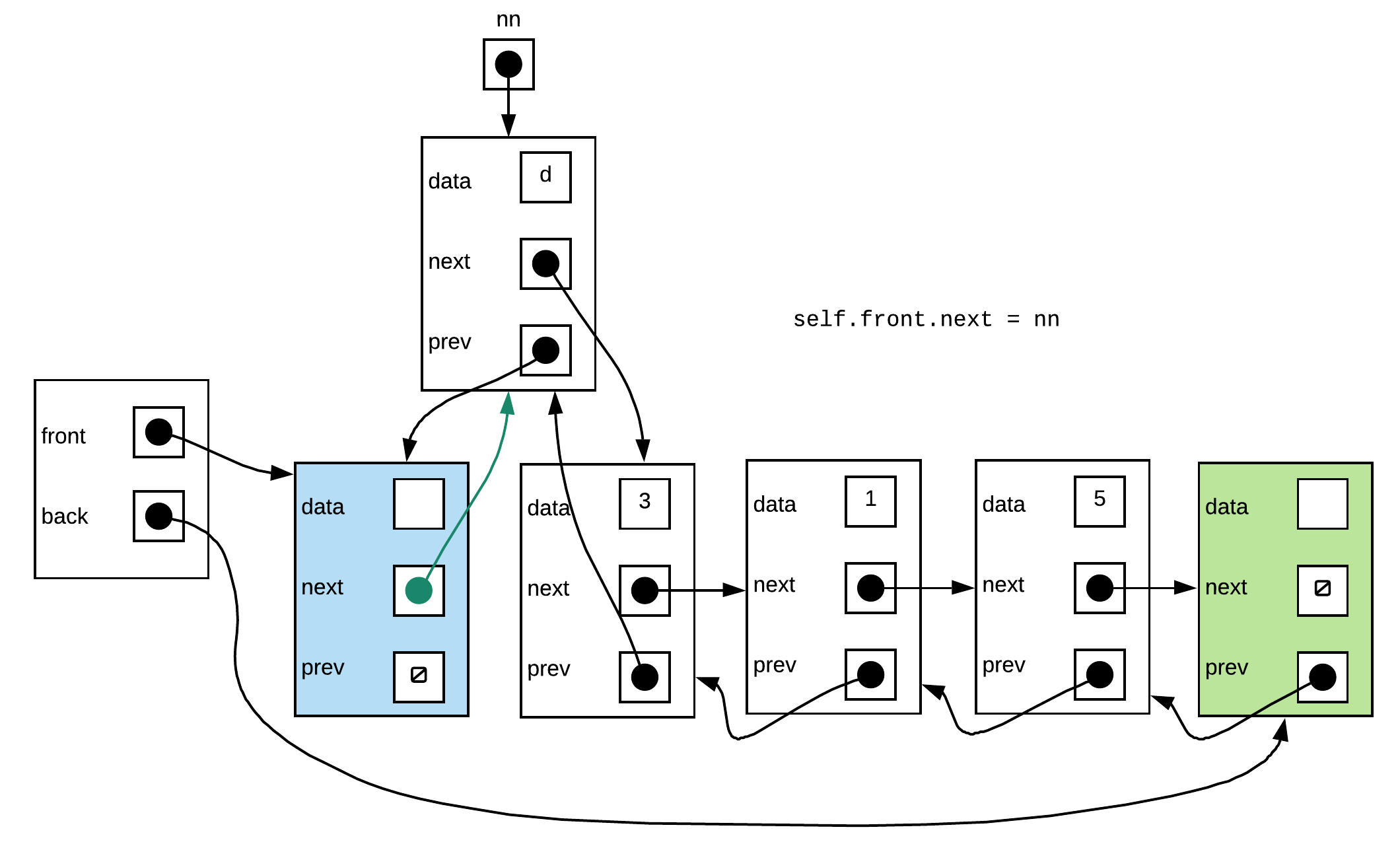
Step 3: Set the next pointer of the front sentinel to the new node.
Does the above always work?
In the non-sentinel version, we know that the function fails for empty linked lists. Does the above function work if you had an linked list that has sentinel nodes?
We begin with an empty linked list with sentinel nodes
Step 1: looks good so far
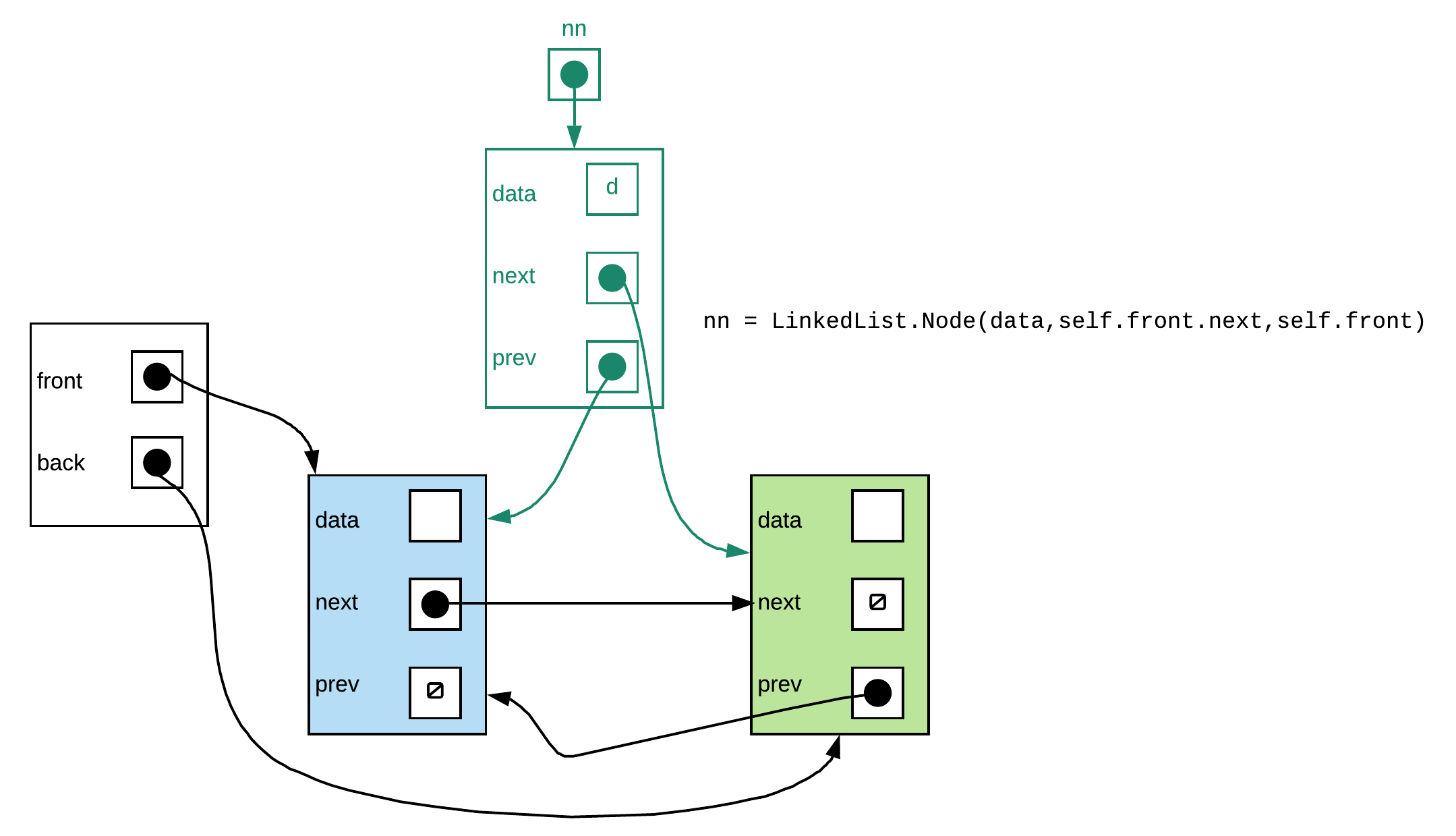
Step 2: No problem here
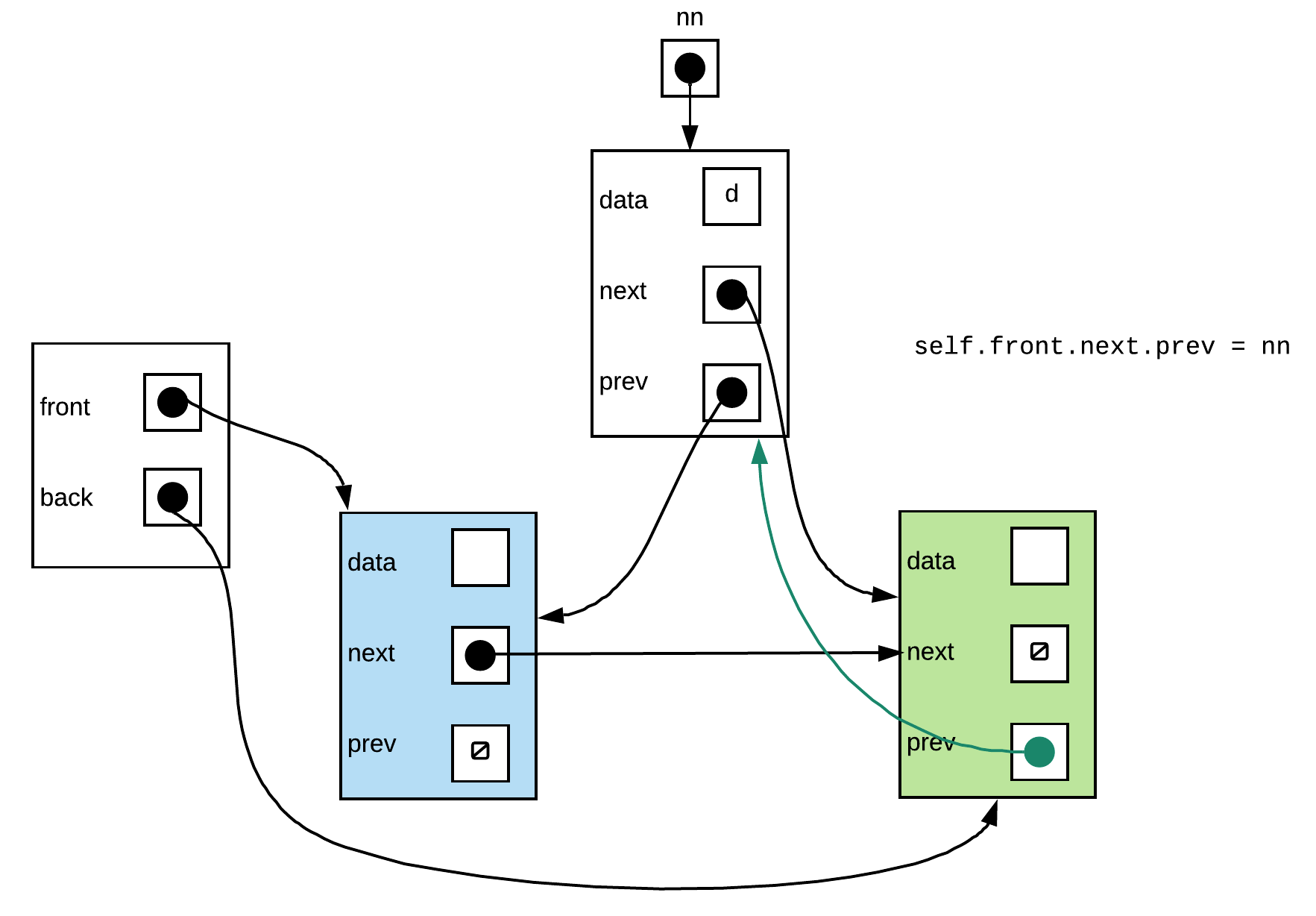
Step 3: and done... a valid linked list
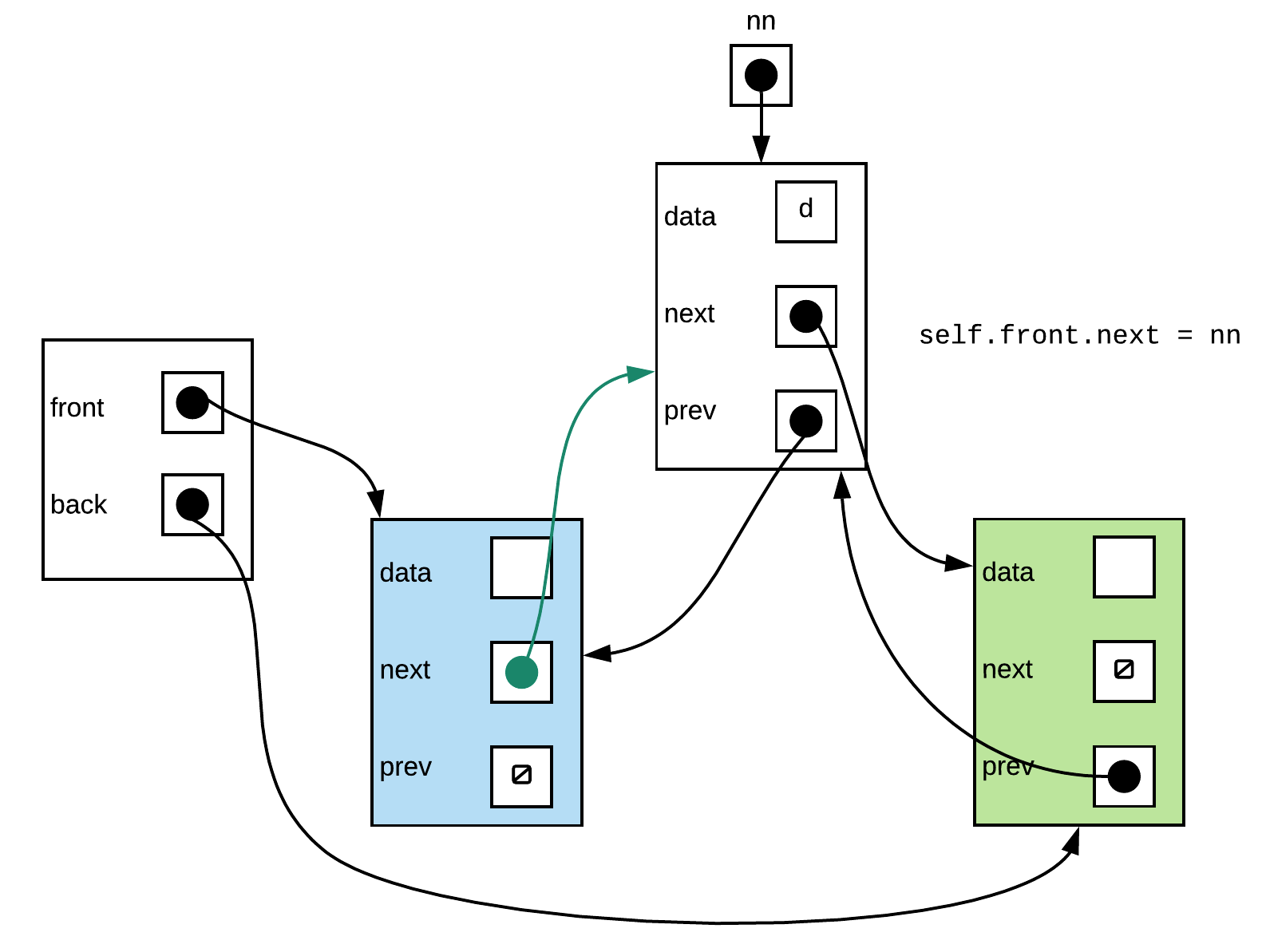
As you can see from above, the same set of steps applied to the general case as well as empty list would end up with a proper linked list. Thus we only need one version of push_front function (3 steps, no special case checks)
def push_front(self, data):
nn = self.Node(data, self.front.next, self.front)
self.front.next.prev = nn
self.front.next = nn
pop_front()
How will we change pop_front() now that we have sentinels?
Step 1: Check to make sure list isn't empty. If it is do nothing. Otherwise continue to next steps. Remember that with sentinels, an empty list still has two nodes (the front and back sentinels). Our empty check is therefore going to look at whether those are the only nodes that exist. We can do this by checking if front sentinel's next_ pointer points to the back sentinel
Step 2: Make a local pointer point to the Node we want to remove. This will be the node that follows the front sentinel as it is the first node with real data. (hold this node so we don't lose it by accident)
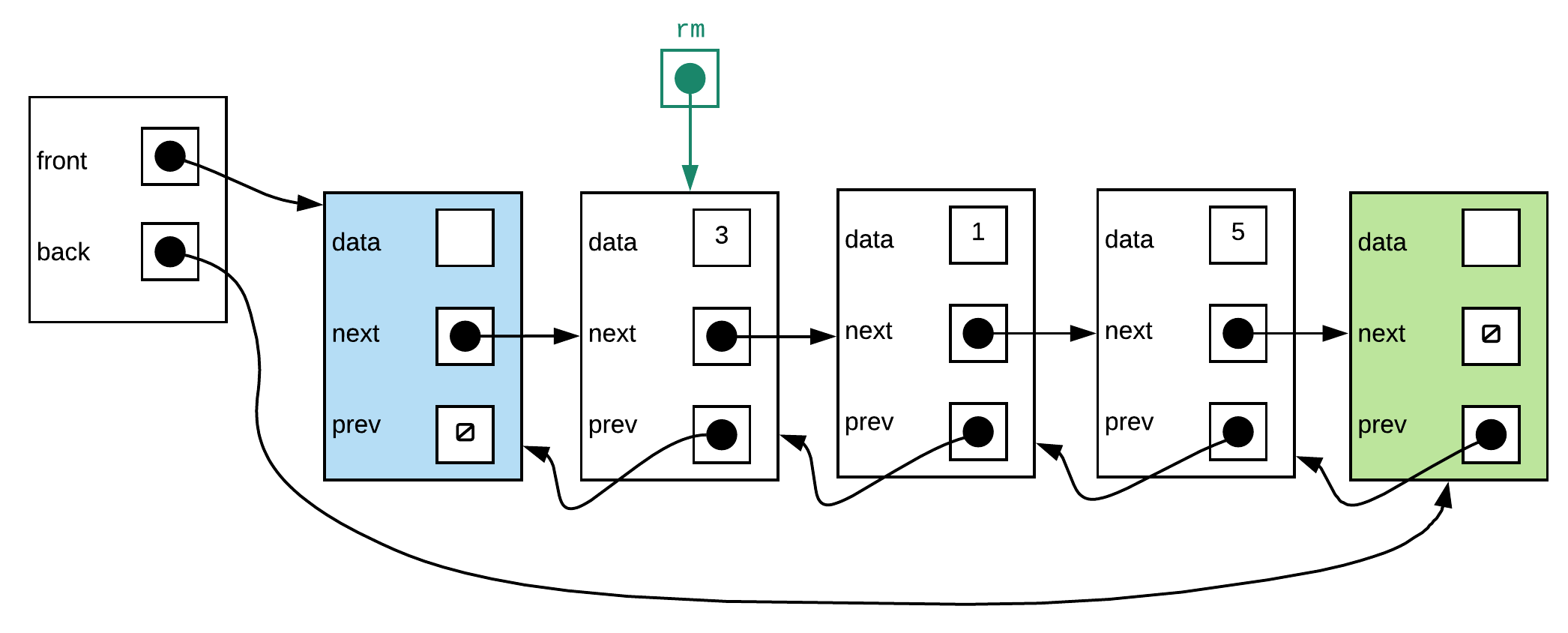
Step 3: Make the front sentinel's next pointer point to second data node (the one that follows the one we want to remove
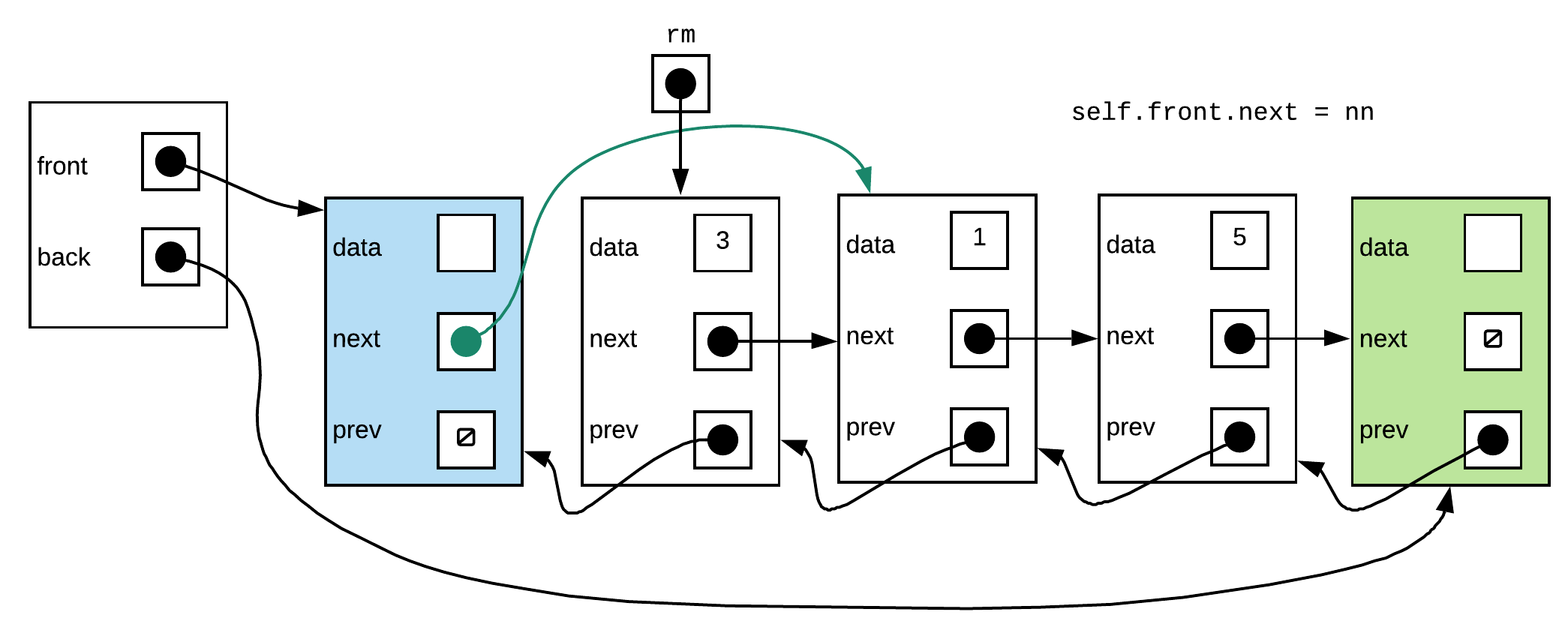
Step 4: Make the previous pointer of the node that now follows the front sentinel point back to the front sentinel
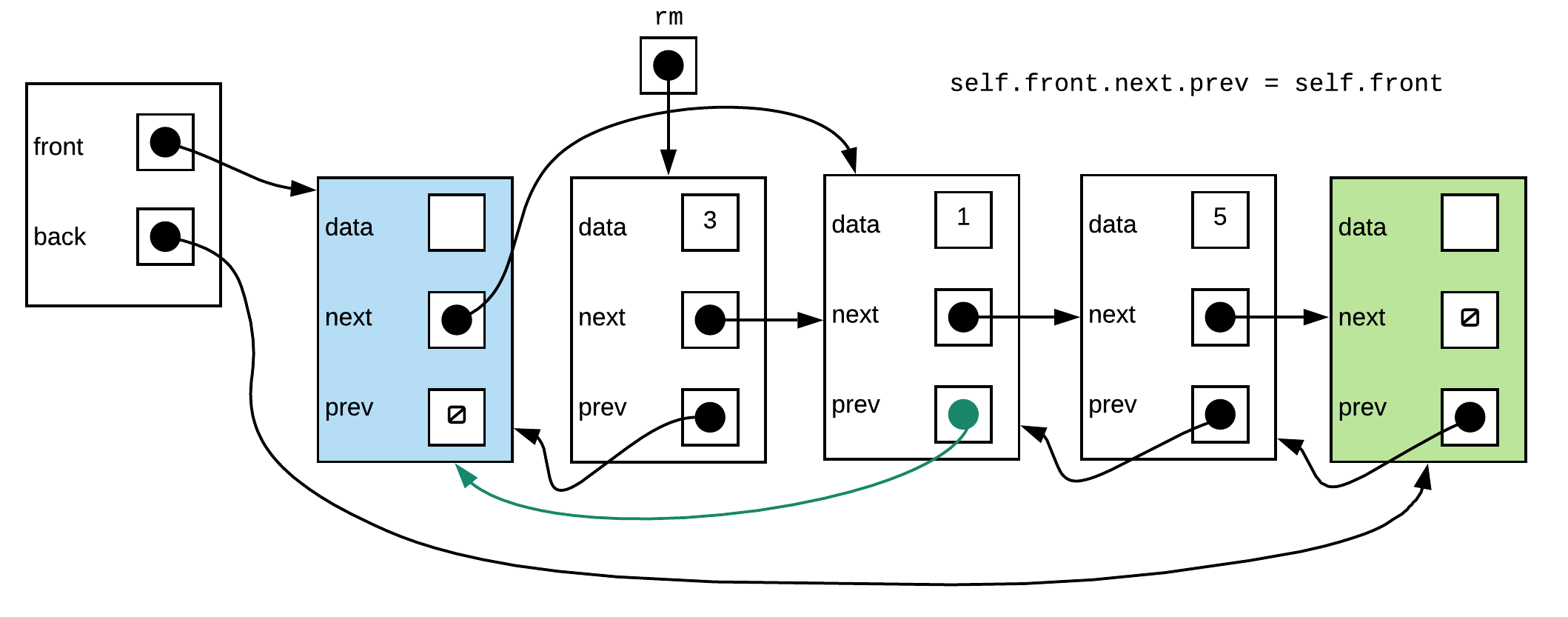
The code snippet to do this is:
if self.front.next is not self.back:
rm = self.front.next
rm.next.prev = rm.prev
rm.prev.next = rm.next
del rm
Does the above always work?
When we looked at the linked list that did not use sentinels we saw that the general solution did not work when the node being removed was the only node left. Question is, will it work now if the node we want to remove is the only one left.
If we perform the four steps inside the if statement from the above snippet, this is what we will see:
Step 2:
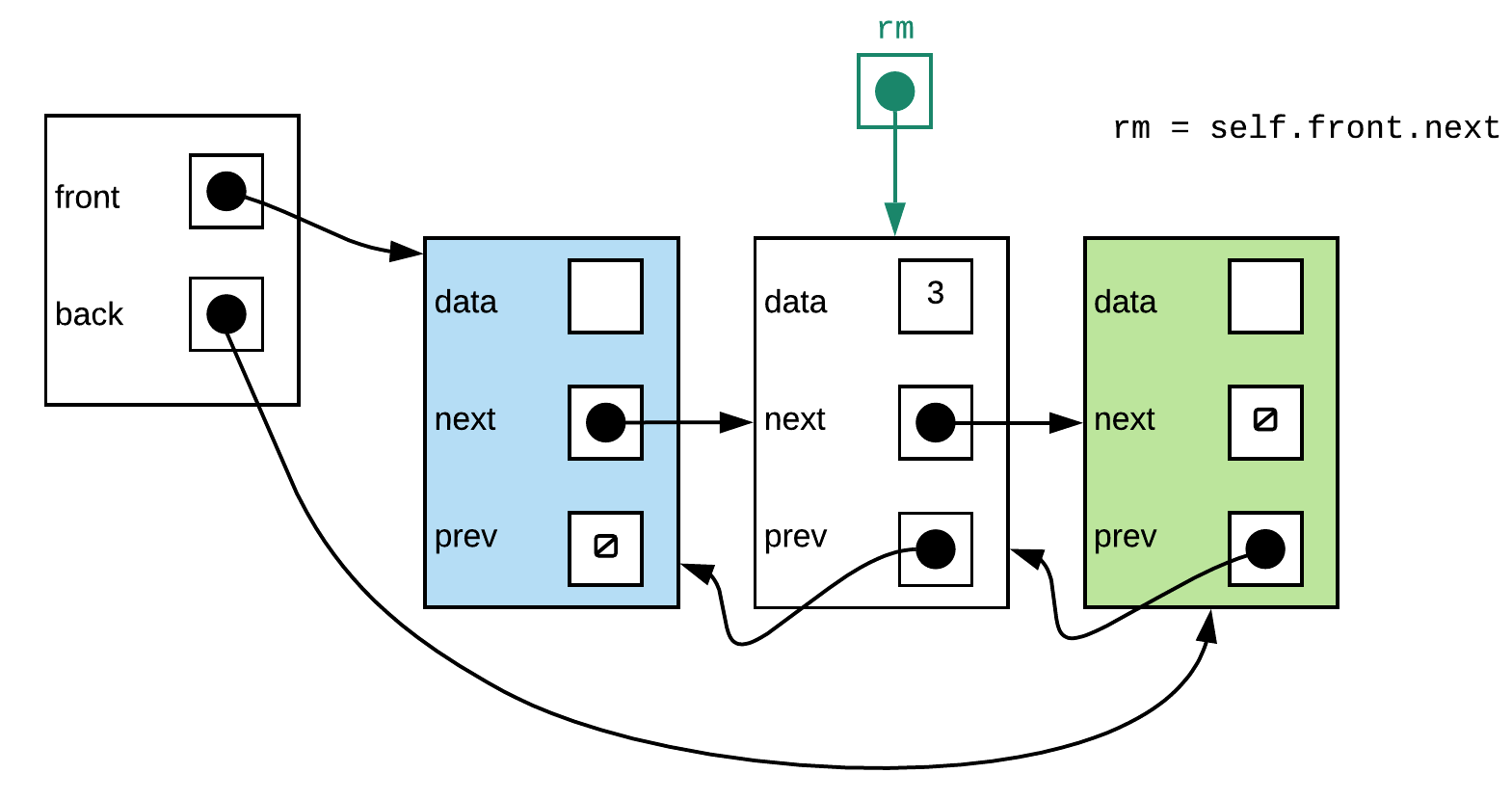
Above looks fine.
Step 3:
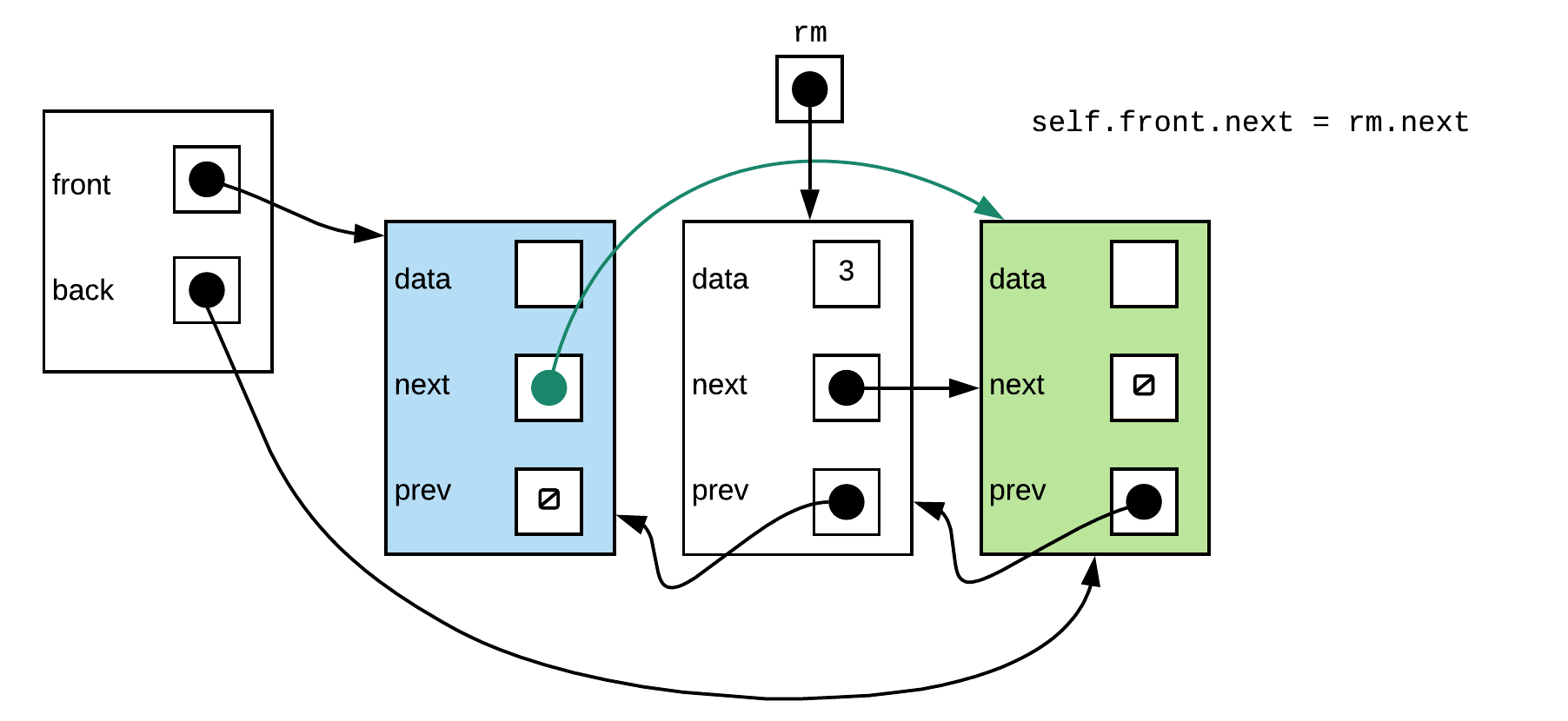
This also looks correct
Step 4:
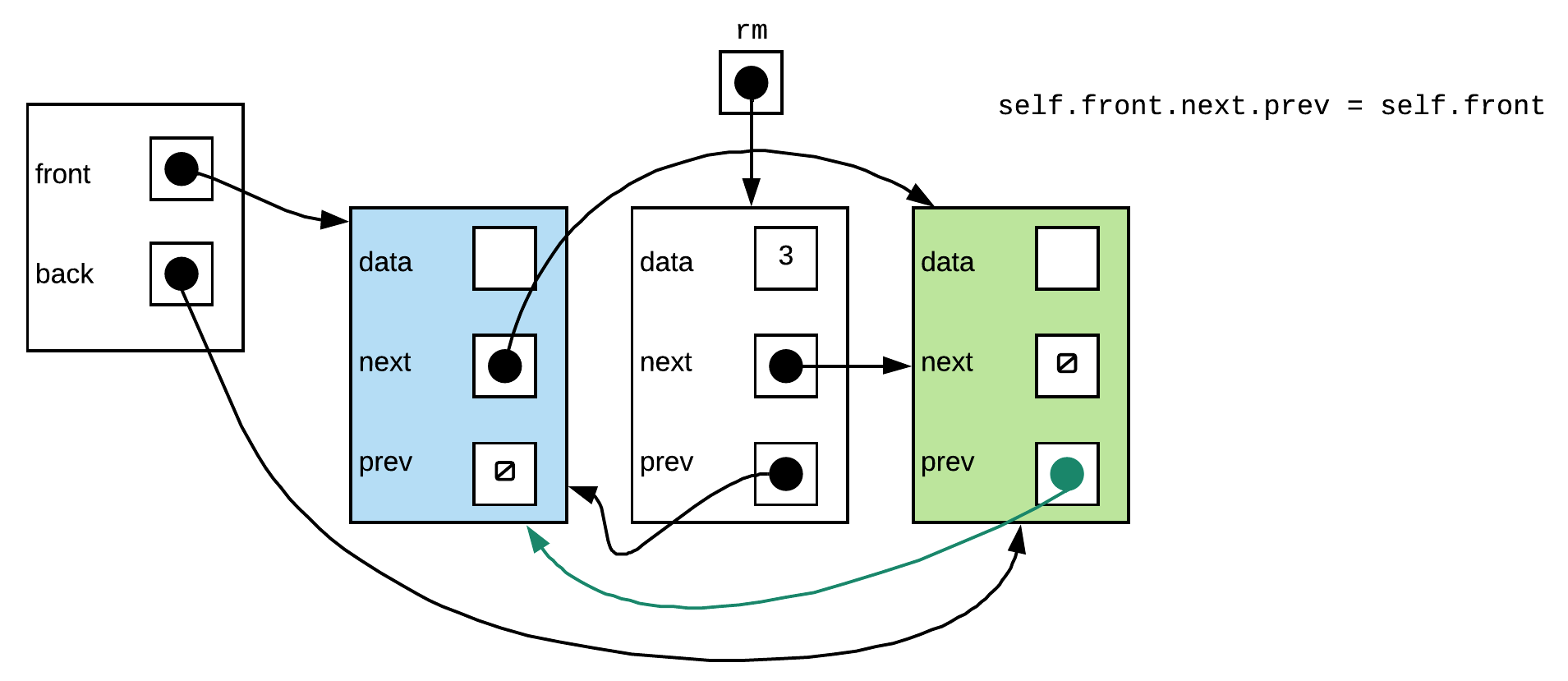
This was a problem in the non-sentinel version but we can see that there isn't a problem here. No nullptr access.
Thus, our function works for both the general and special case.
Putting all this together our pop_front() function should look something like this:
def pop_front(self):
if self.front.next is not self.back:
rm = self.front.next
rm.next.prev = rm.prev
rm.prev.next = rm.next
del rm
template <typename T>
class DList{
struct Node{
T data;
Node* next;
Node* prev;
Node(const T& dat=T{}, Node* nx=nullptr, Node* pr=nullptr){
data=dat;
next=nx;
prev=pr;
}
};
Node* front;
Node* back;
public:
DList(){
front = new Node();
back = new Node();
front->next=back;
back->prev=front;
}
};
push_front()
How will push_front change with sentinels?
Step 1: Create new node, next node is the node that follows the front sentinel. The previous node is the front sentinel.
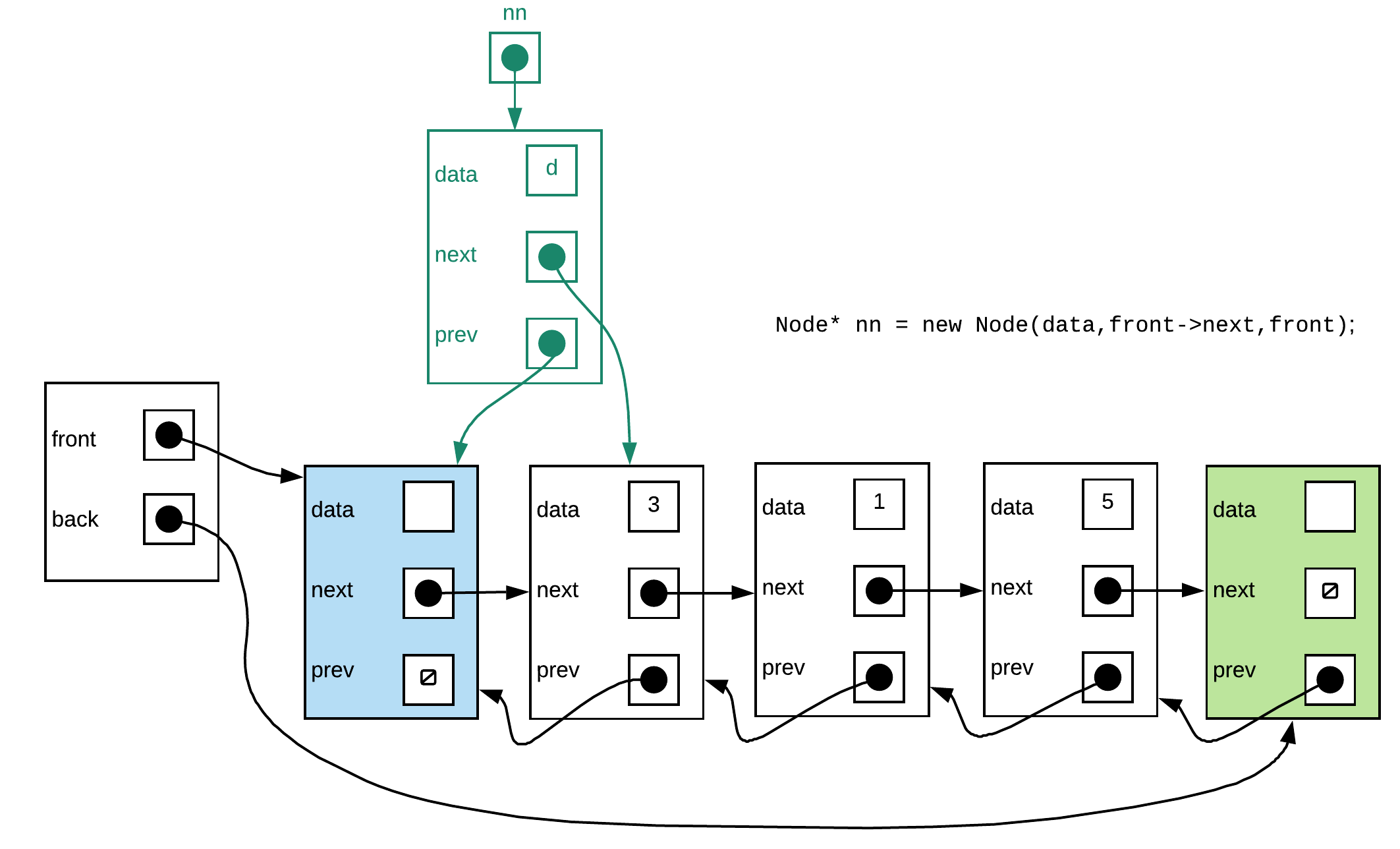
Step 2: Make the previous pointer of the node that follows the front sentinel point to the new node
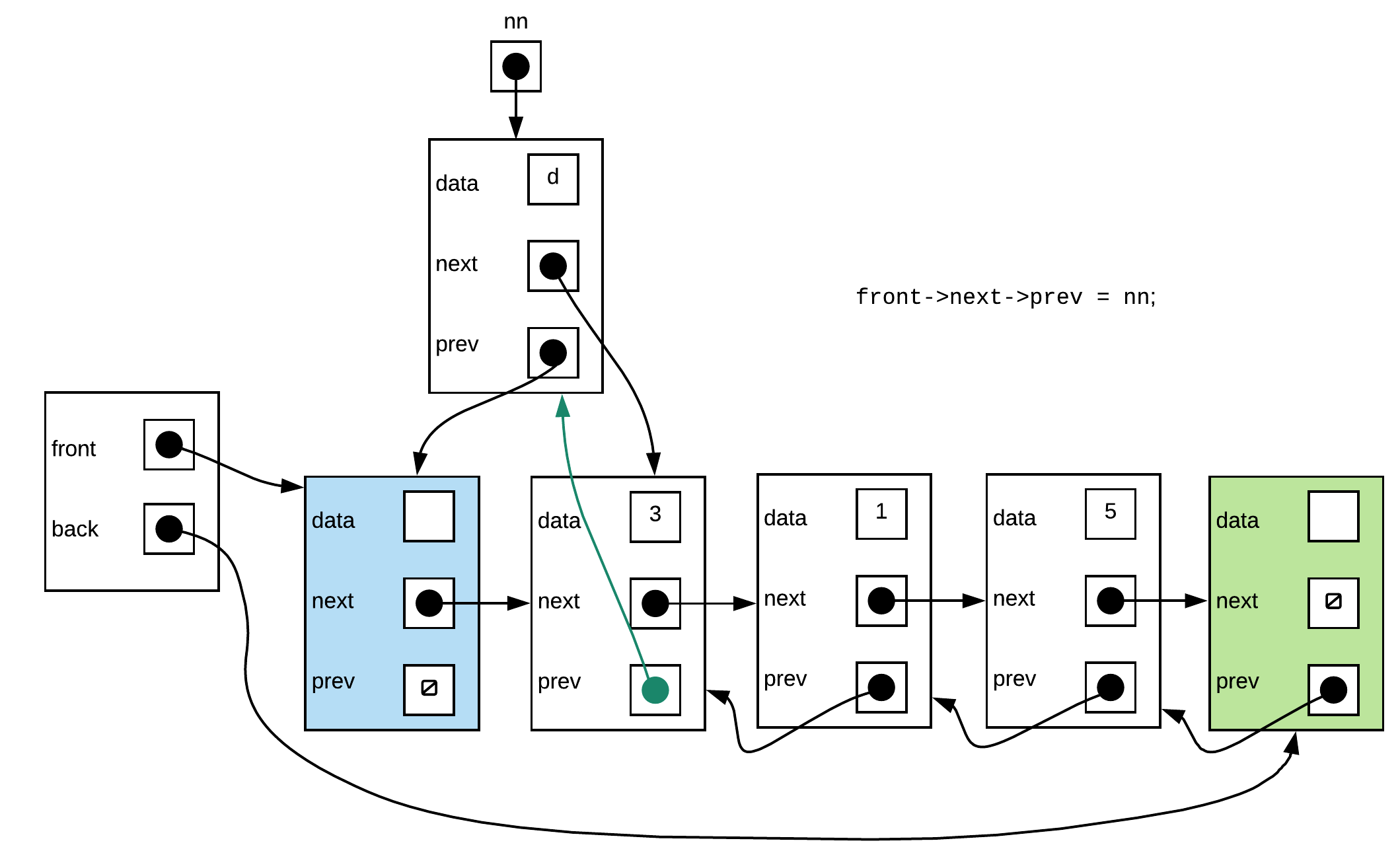
Step 3: Set the next pointer of the front sentinel to the new node.
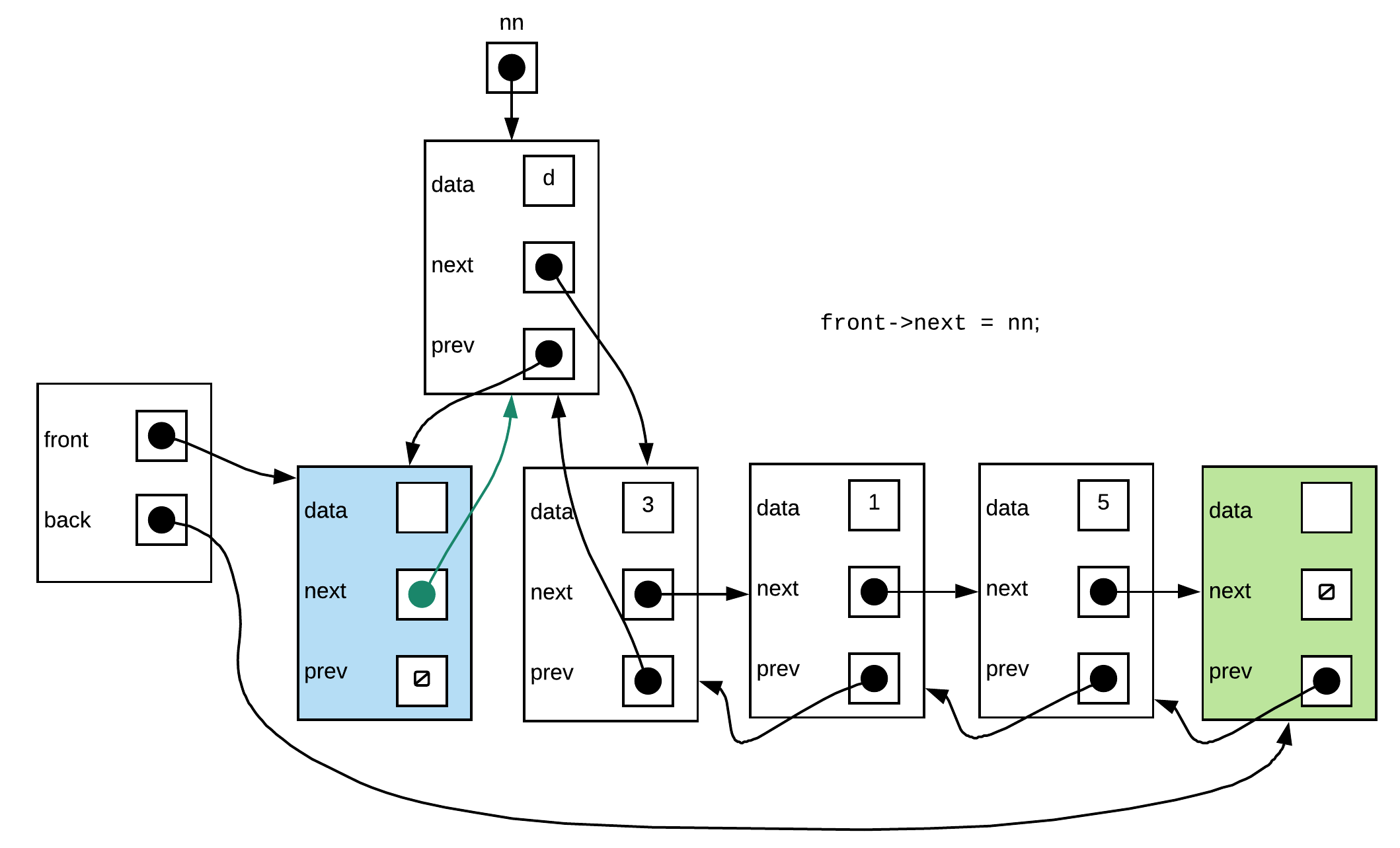
Does the above always work?
In the non-sentinel version, we know that the function fails for empty linked lists. Does the above function work if you had an linked list that has sentinel nodes?
We begin with an empty linked list with sentinel nodes
Step 1: looks good so far
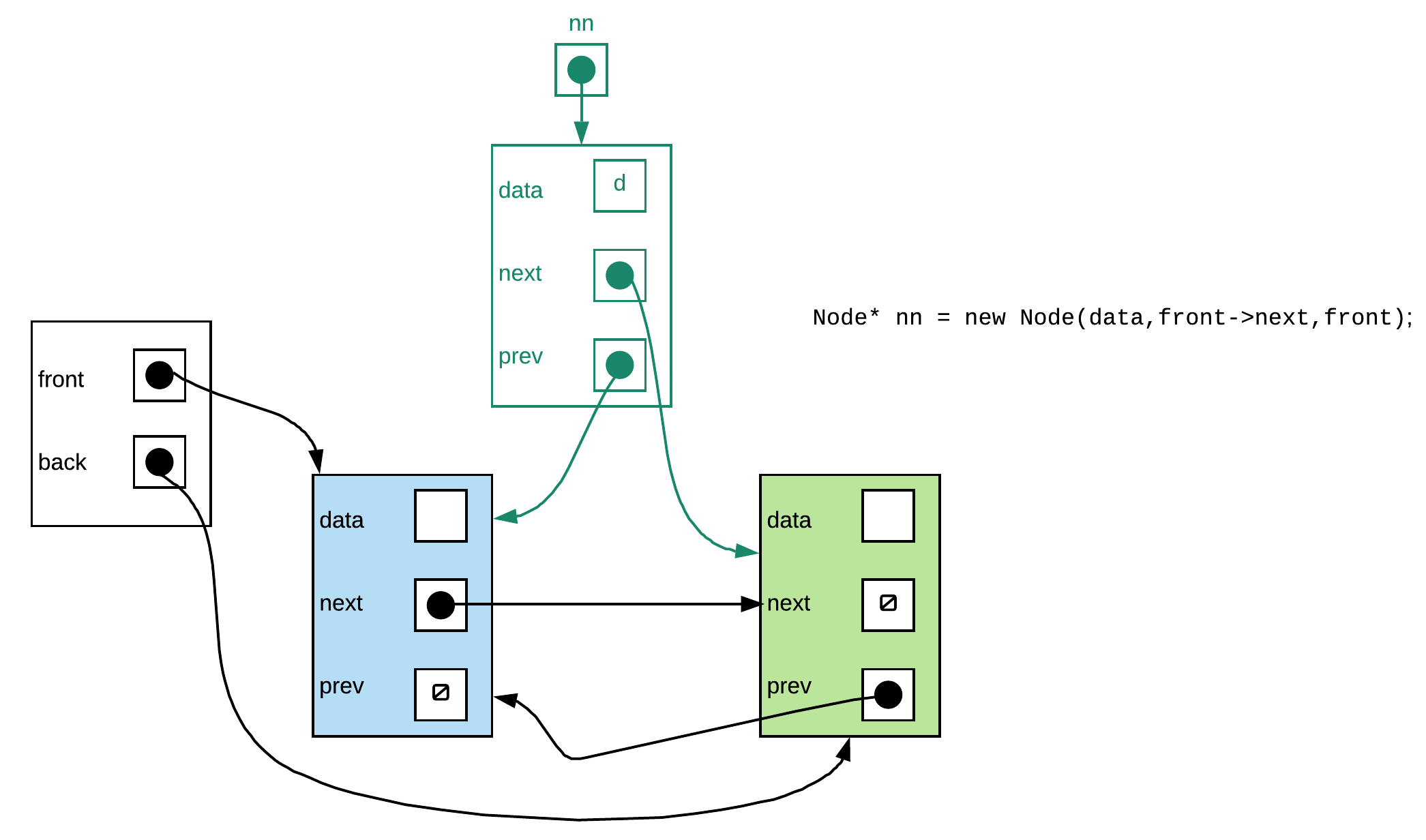
Step 2: No problem here
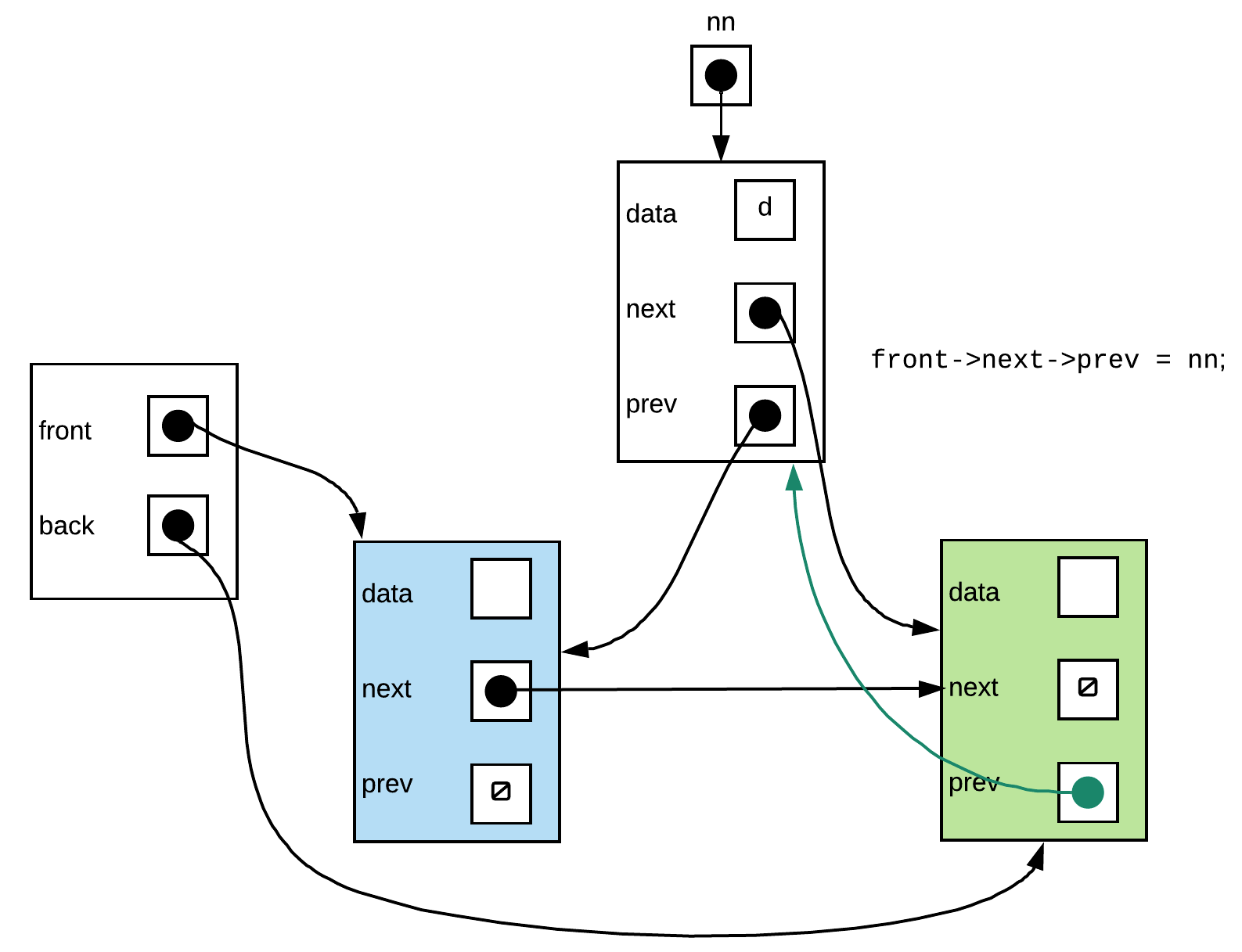
Step 3: and done... a valid linked list
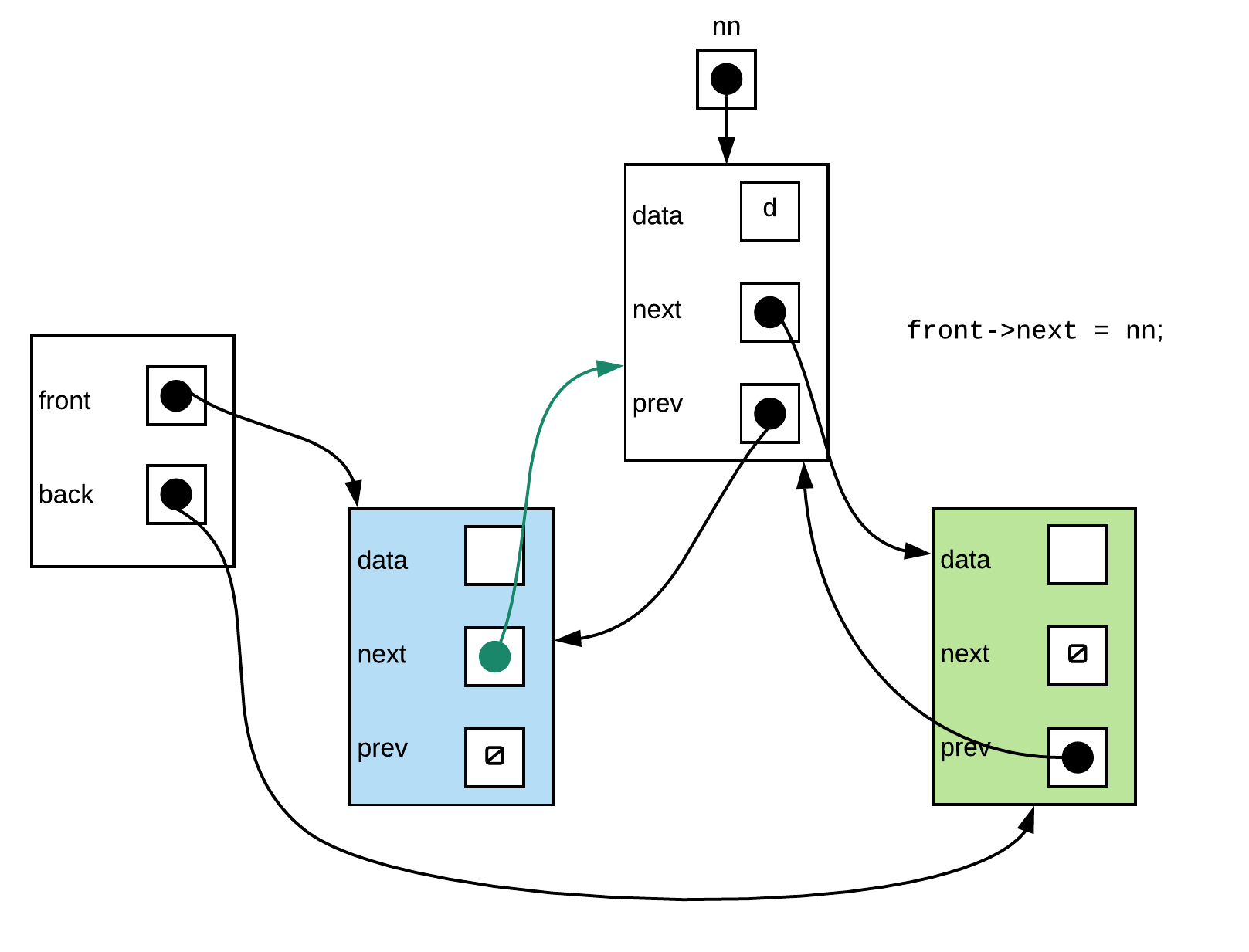
As you can see from above, the same set of steps applied to the general case as well as empty list would end up with a proper linked list. Thus we only need one version of push_front function (3 steps, no special case checks)
void push_front(const T& data){
Node* nn=new Node(data,front->next,front);
front->next->prev = nn;
front->next = nn;
}
pop_front()
How will we change pop_front() now that we have sentinels?
Step 1: Check to make sure list isn't empty. If it is do nothing. Otherwise continue to next steps. Remember that with sentinels, an empty list still has two nodes (the front and back sentinels). Our empty check is therefore going to look at whether those are the only nodes that exist. We can do this by checking if front sentinel's next_ pointer points to the back sentinel
Step 2: Make a local pointer point to the Node we want to remove. This will be the node that follows the front sentinel as it is the first node with real data. (hold this node so we don't lose it by accident)

Step 3: Make the front sentinel's next pointer point to second data node (the one that follows the one we want to remove
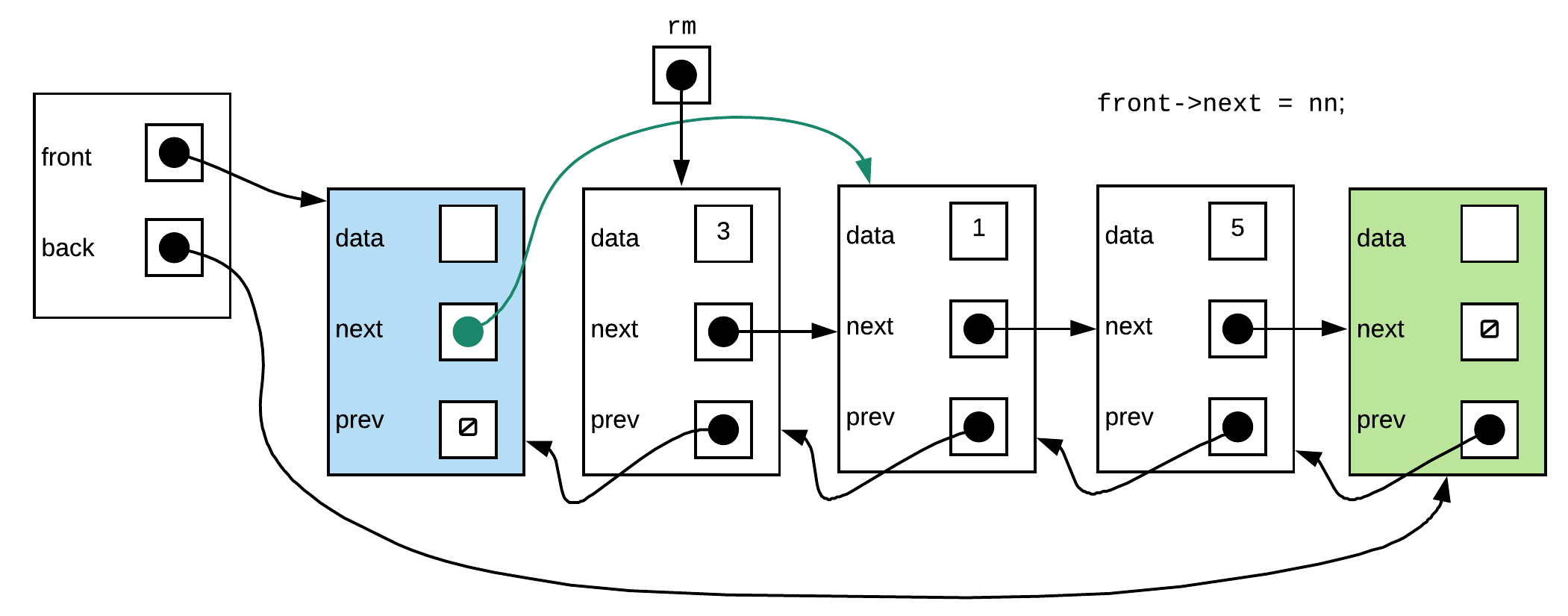
Step 4: Make the previous pointer of the node that now follows the front sentinel point back to the front sentinel
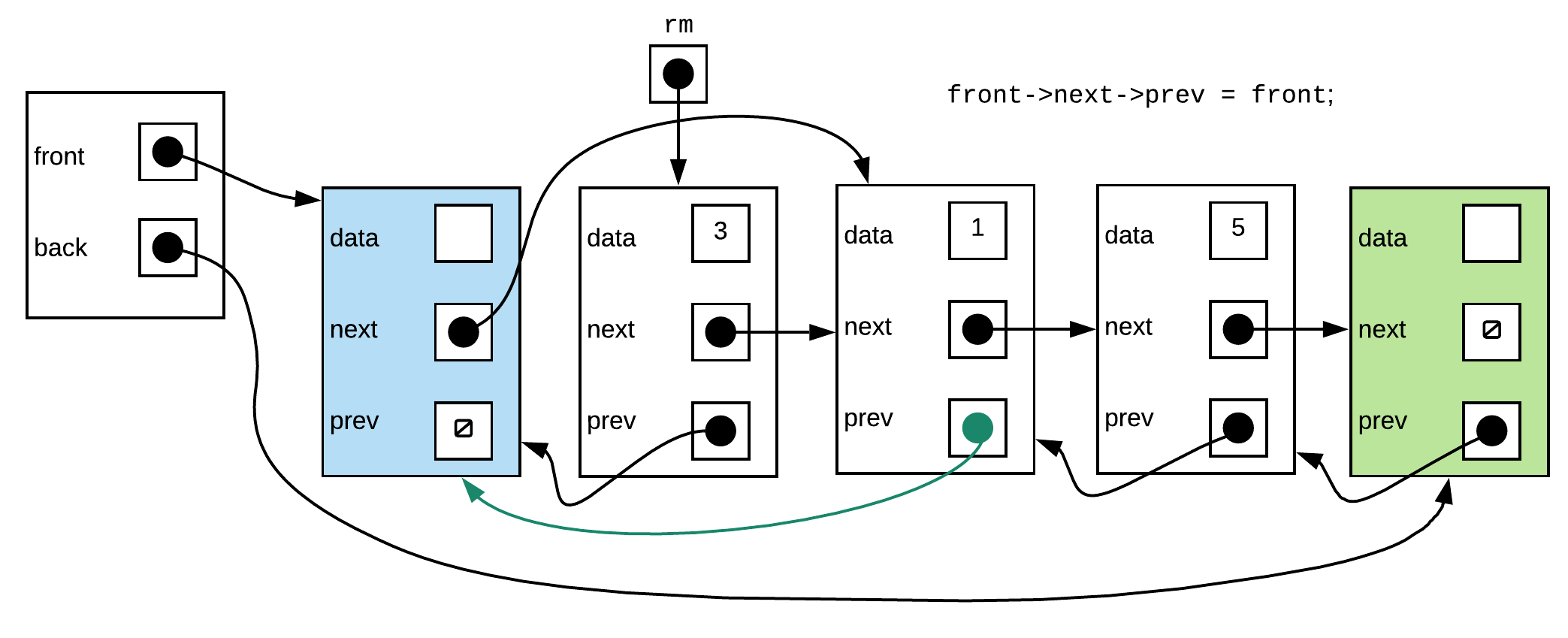
Step 5: deallocate the node we are removing
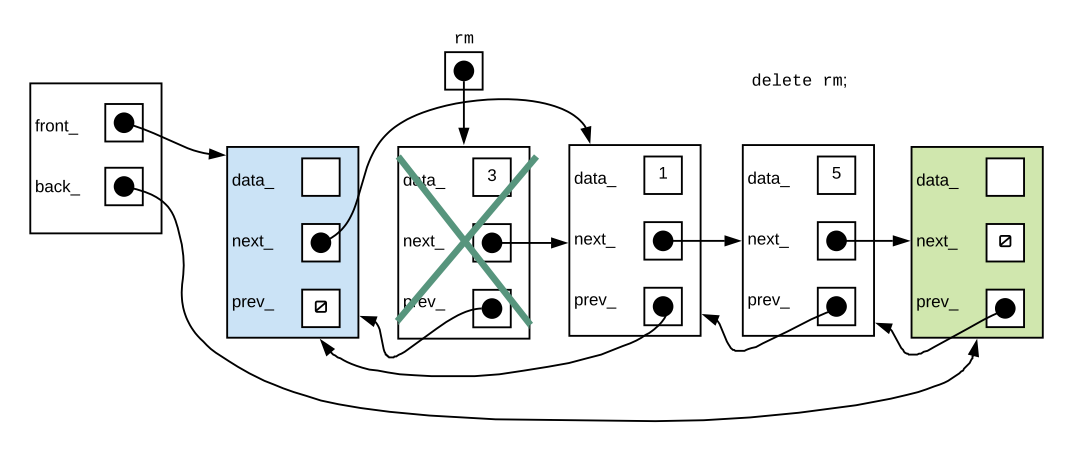
The code snippet to do this is:
if(front->next != back_){ //check for empty list
Node* rm = front->next;
front->next=rm->next;
front->next->prev=front;
delete rm;
}
Does the above always work?
When we looked at the linked list that did not use sentinels we saw that the general solution did not work when the node being removed was the only node left. Question is, will it work now if the node we want to remove is the only one left.
If we perform the four steps inside the if statement from the above snippet, this is what we will see:
Step 2:
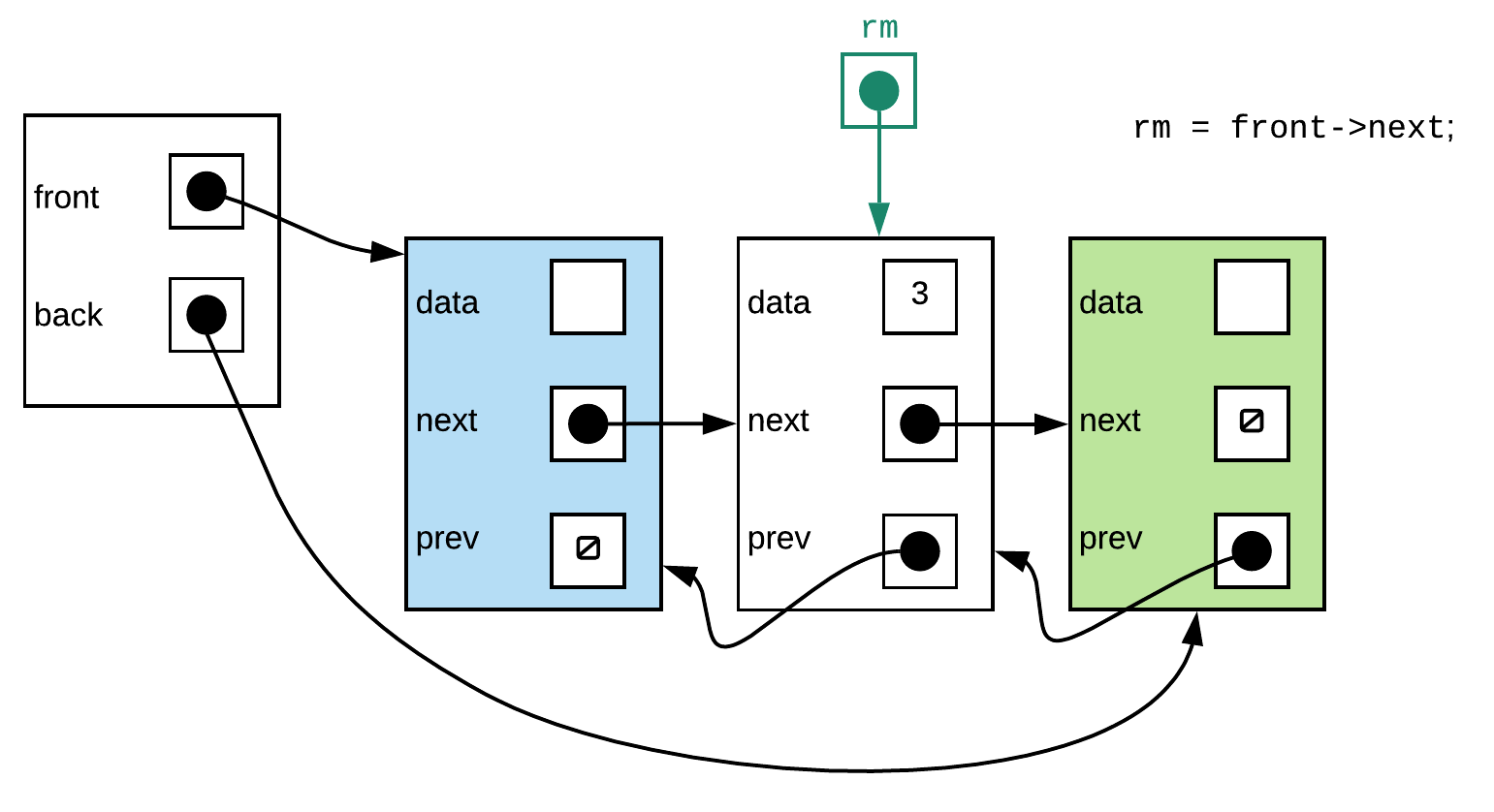
Above looks fine.
Step 3:
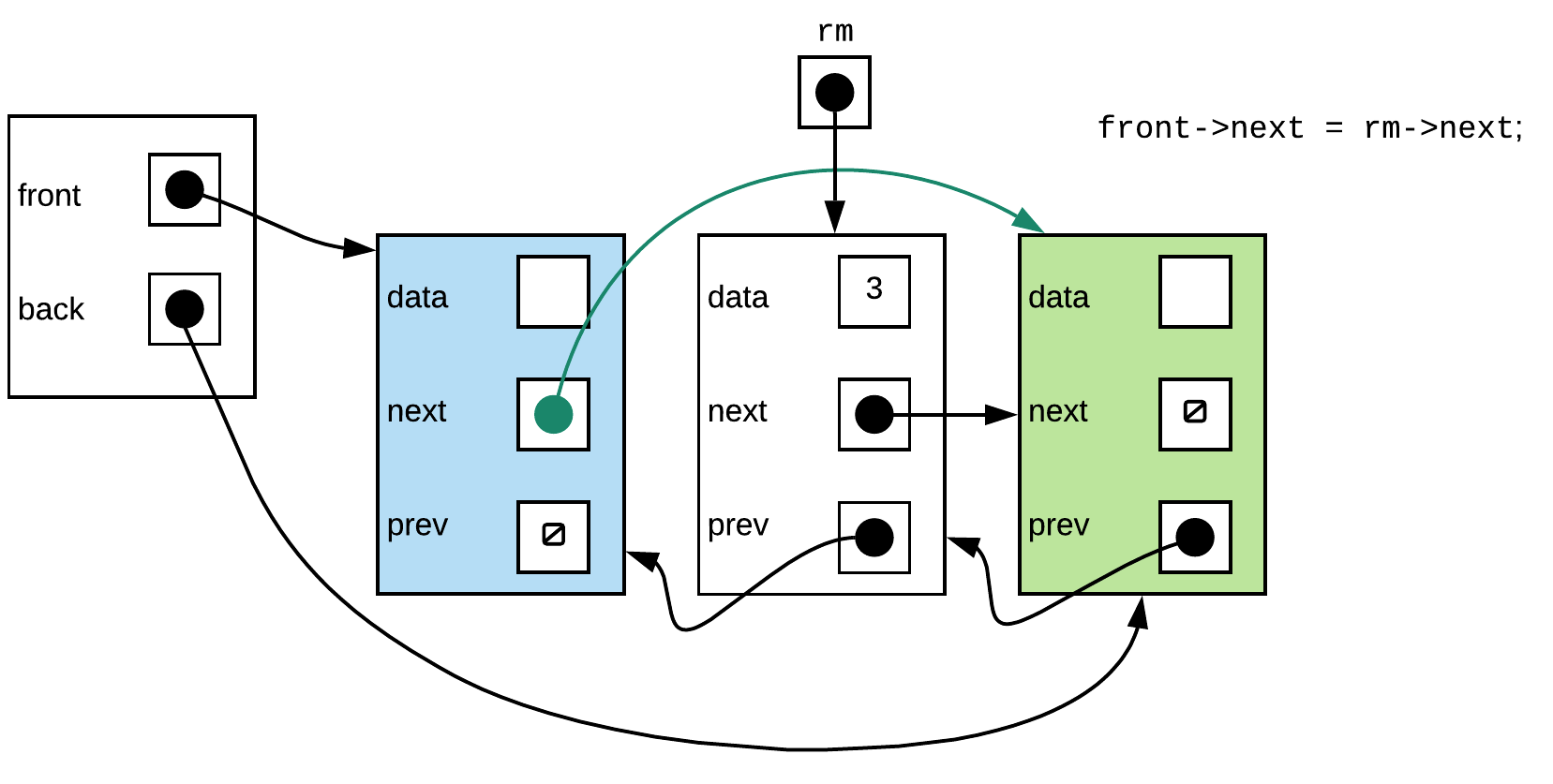
This also looks correct
Step 4:
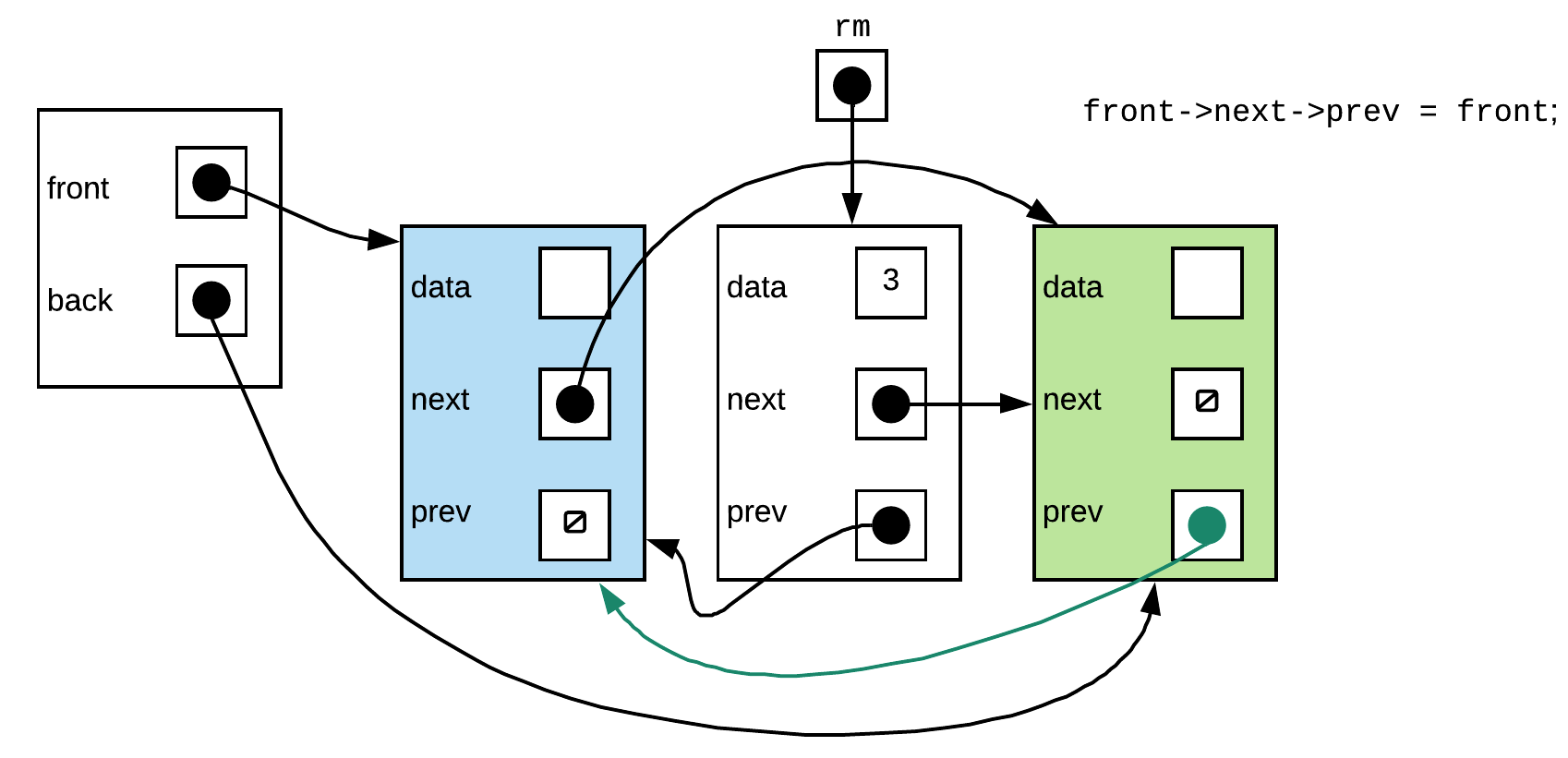
This was a problem in the non-sentinel version but we can see that there isn't a problem here. No nullptr access.
Step 5:
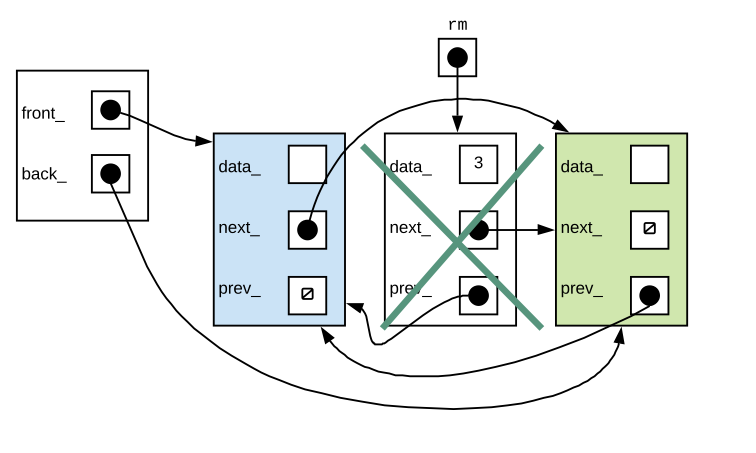
The final line is to delete the node. Notice now, that our list is essentially an empty linked list (with just the two sentinels). Thus, our function works for both the general and special case.
Putting all this together our pop_front() function should look something like this:
void pop_front(){
if(front->next != back){ //check for empty list
Node* rm = front->next;
front->next = rm->next;
front->next->prev = front;
delete rm;
}
}