Iterative Methods
This section looks at the functions that are implemented iteratively (or the iterative version of the functions)
Insert - Iterative version
This function will insert data into the tree. There are two ways to implement this function, either iteratively or recursively. We will start by looking at the iterative solution. In this situation, we begin by taking care of the empty tree situation. If the tree is empty we simply create a node and make root_ point to that only node. Otherwise, we need to go down our tree until we find the place where we must do the insertion and then create the node.
- Python
- C++
class BST:
class Node:
# Node's init function
def __init__(self, data=None, left=None, right=None):
self.data = data
self.left = left
self.right = right
# BST's init function
def __init__(self):
self.root = None
def insert(self, data):
if self.root is None:
self.root = BST.Node(data)
else:
# curr points to the variable we are currently looking at
curr = self.root
inserted = False
while not inserted:
if data < curr.data:
if curr.left is not None:
curr = curr.left
else:
curr.left = BST.Node(data)
inserted = True
else:
if curr.right is not None:
curr = curr.right
else:
curr.right = BST.Node(data)
inserted = True
template <typename T>
class BST{
struct Node{
T data_;
Node* left_;
Node* right_;
Node(const T& data, Node* left=nullptr, Node* right=nullptr){
data_=data;
left_=left;
right_=right;
}
};
//single data member pointing to root of tree
Node* root_;
public:
...
void insert(const T& data){
if(root_==nullptr){
root_=new Node(data);
}
else{
bool isInserted=false; //set to true when once we insert the node
Node* curr=root_; //used to iterate through nodes
while(!isInserted){
if(data < curr->data_){
//data belongs in left subtree because it is
//smaller than current node
if(curr->left_){
//there is a node to the left so go left
curr=curr->left_;
}
else{
//there isn't a node to left
//create a node to the left
curr->left_=new Node(data);
isInserted=true;
}
}
else{
//data belongs in right subtree.
if(curr->right_){
//there is a node to the right so go right
curr=curr->right_;
}
else{
//there isn't a node to right
//create a node to the right
curr->right_=new Node(data);
isInserted=true;
}
}
}
}
}
...
};
Search - Iterative version
The key operation that is supported by a binary search tree is search. For our purposes we will simply look at finding out whether or not a value is in the tree or not. The search operation should never look at the entire tree. The whole point of the binary search tree is to make this operation fast. We should search it so that we can eliminate a portion of the tree with every search operation.
To do this we start at the root and compare that node's data against what we want. If it matches, we have found it. If not, we go either left or right depending on how data relates to the current node. If at any point we have an empty tree (ie the pointer we are using for iterating through the tree becomes nullptr) we stop the search and return false. If we find a node that matches we stop and return true.
- Python
- C++
class BST:
class Node:
# Node's init function
def __init__(self, data=None, left=None, right=None):
self.data = data
self.left = left
self.right = right
# BST's init function
def __init__(self):
self.root = None
def search(self, data):
curr = self.root
while curr is not None:
if data < curr.data:
curr = curr.left
elif data > curr.data:
curr = curr.right
else:
return curr
return None
template <typename T>
class BST{
struct Node{
T data_;
Node* left_;
Node* right_;
Node(const T& data, Node* left=nullptr, Node* right=nullptr){
data_=data;
left_=left;
right_=right;
}
};
//single data member pointing to root of tree
Node* root_;
public:
bool search(const T& data) const {
Node* curr=root_; //used to iterate through tree
bool found=false; //true if we find it false if we haven't yet
//loop until we either find it or we have no more tree
while(!found && curr){
if(data==curr->data_){
found=true;
}
else if(data < curr->data_){
curr=curr->left_;
}
else{
curr=curr->right_;
}
}
return found;
}
};
Breadth First Print
Writing a breadth-first traversal involves using the queue data structure to order what nodes to deal with next. You want to deal with the nodes from top to bottom left to right, and thus you use the queue to order the nodes. Here is an example of how we will do this.
We begin by declaring a queue (initially empty)
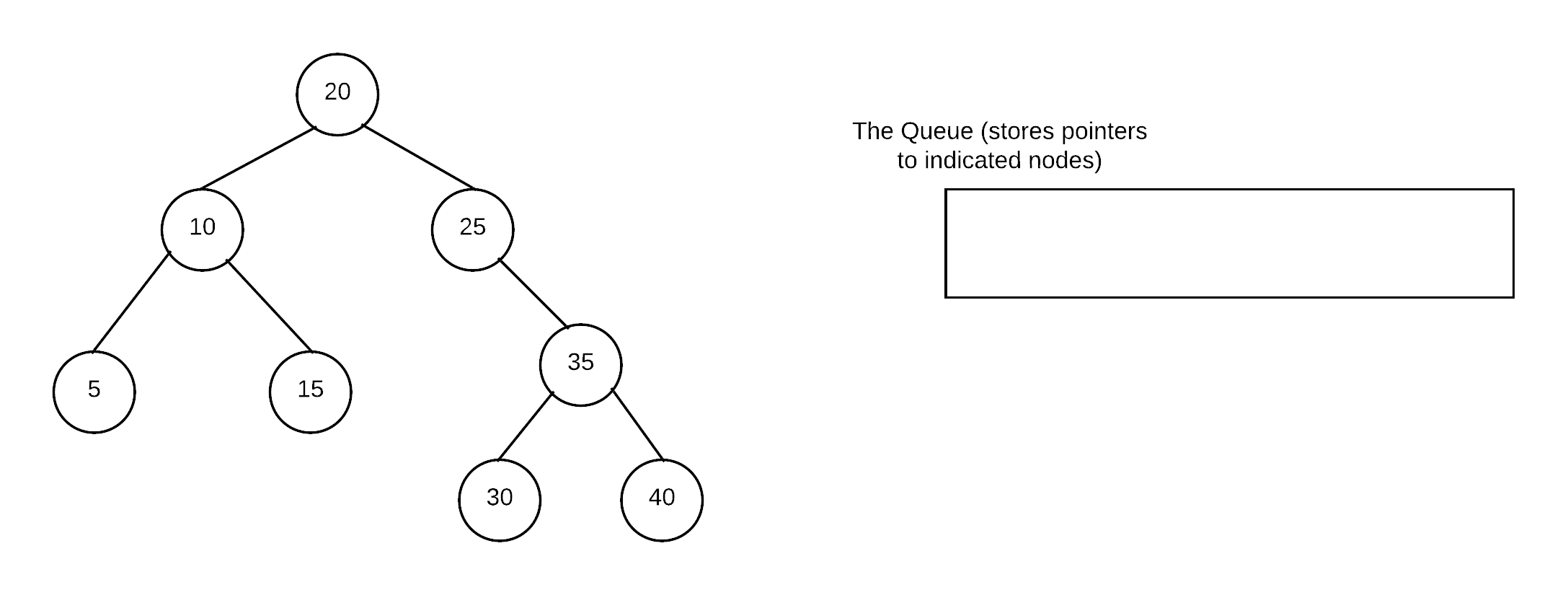
Prime the Queue
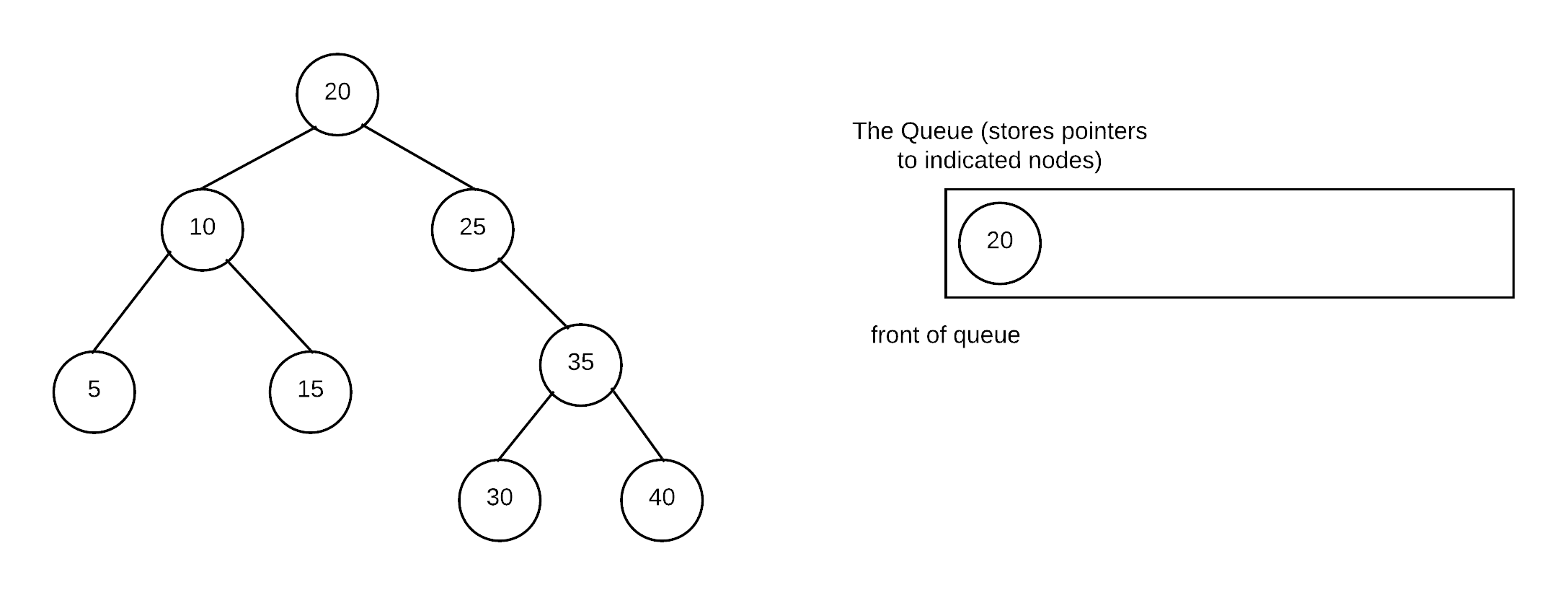
We start prime the queue by putting the root into the queue. In this example, we always check to ensure no nullptrs are ever added to the queue. Alternatively we allow the addition of nullptrs and decide how to deal with them when we dequeue.
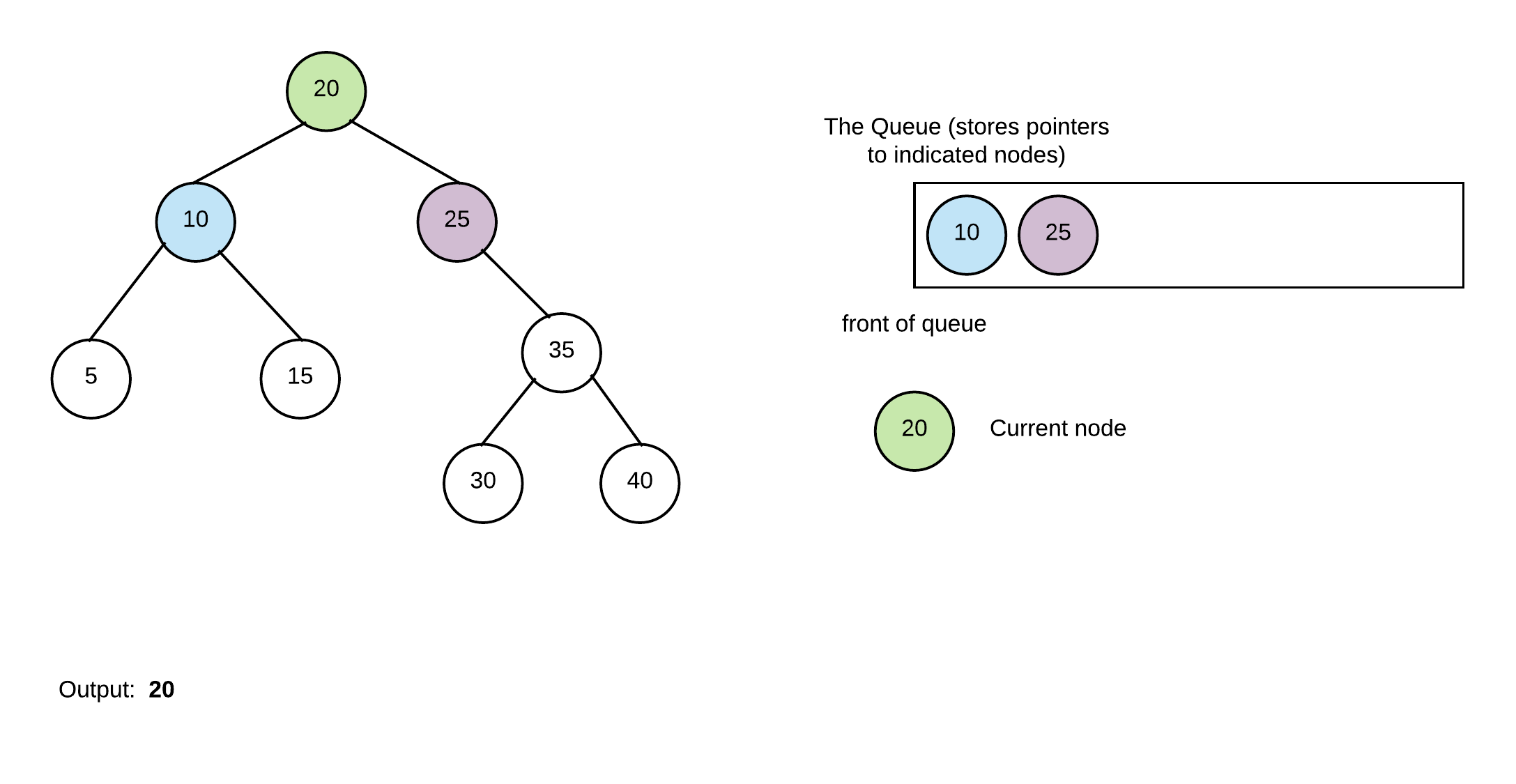
Dequeue front of node and process it by adding its non-nullptr children into the queue, print the node
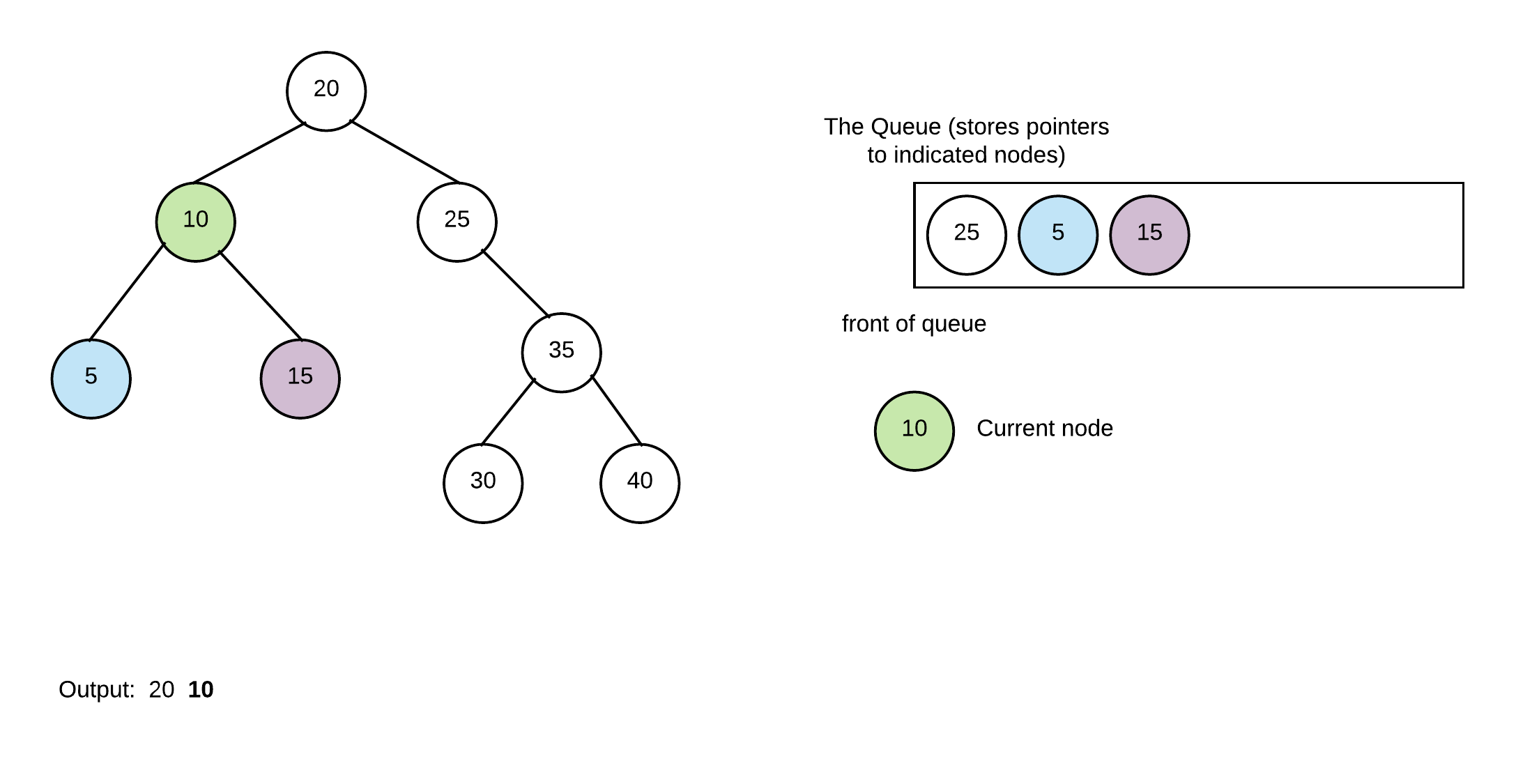
Continue by dequeuing front node and processing it in same manner
Repeat again as 25 only has a right child only it is added
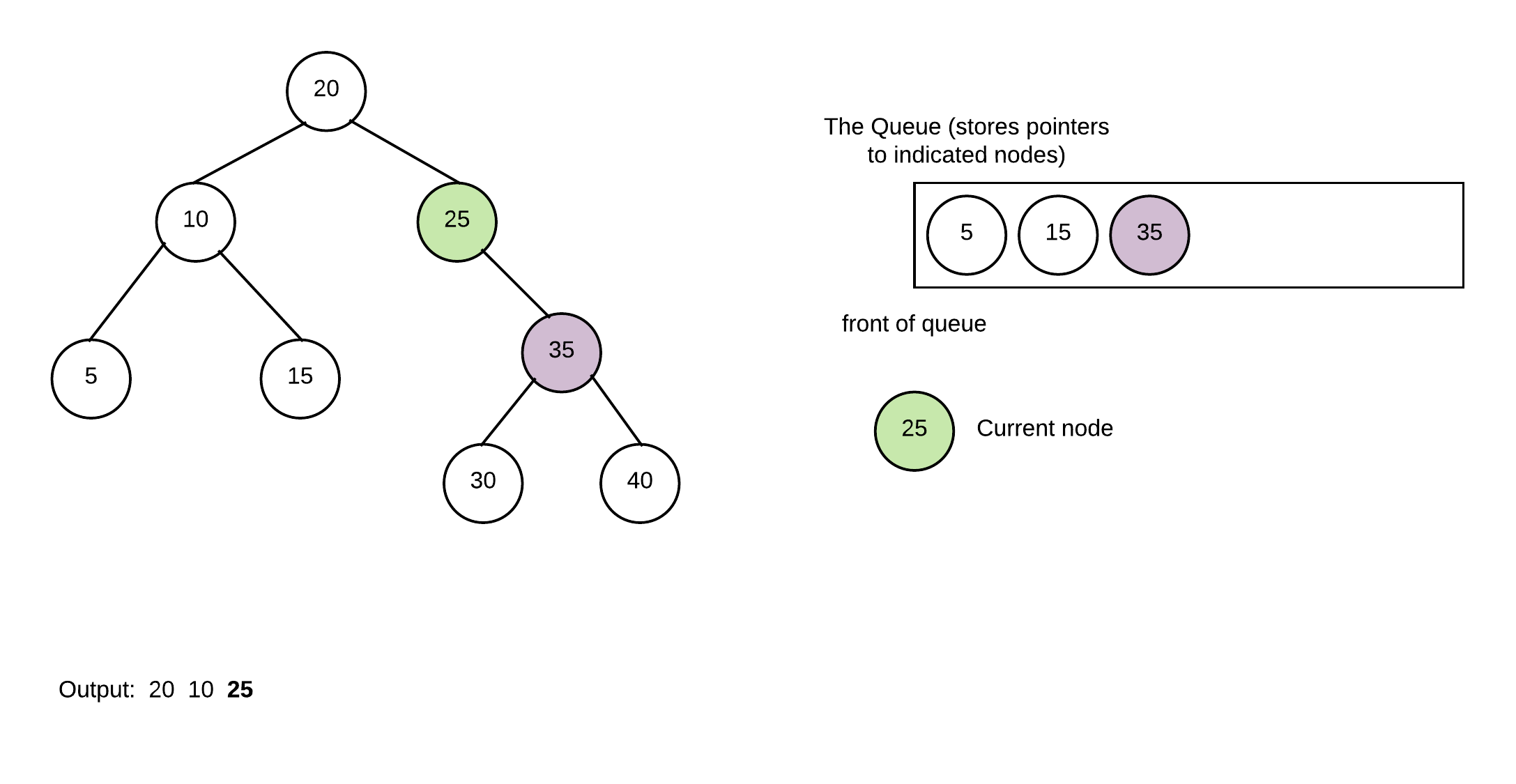
Repeat once again with 5 which has no children thus nothing is added to queue
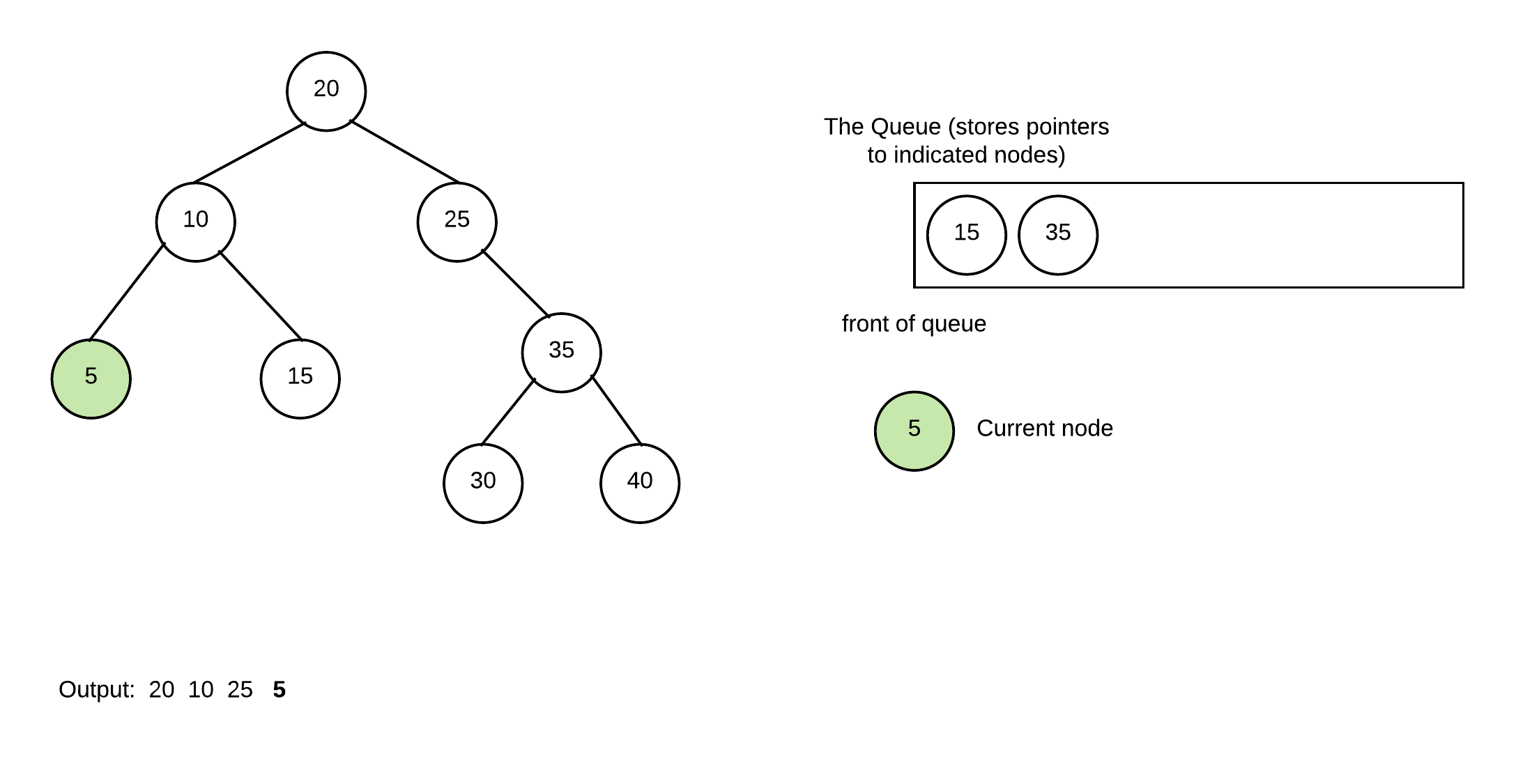
Repeat again with 15 (also no children)
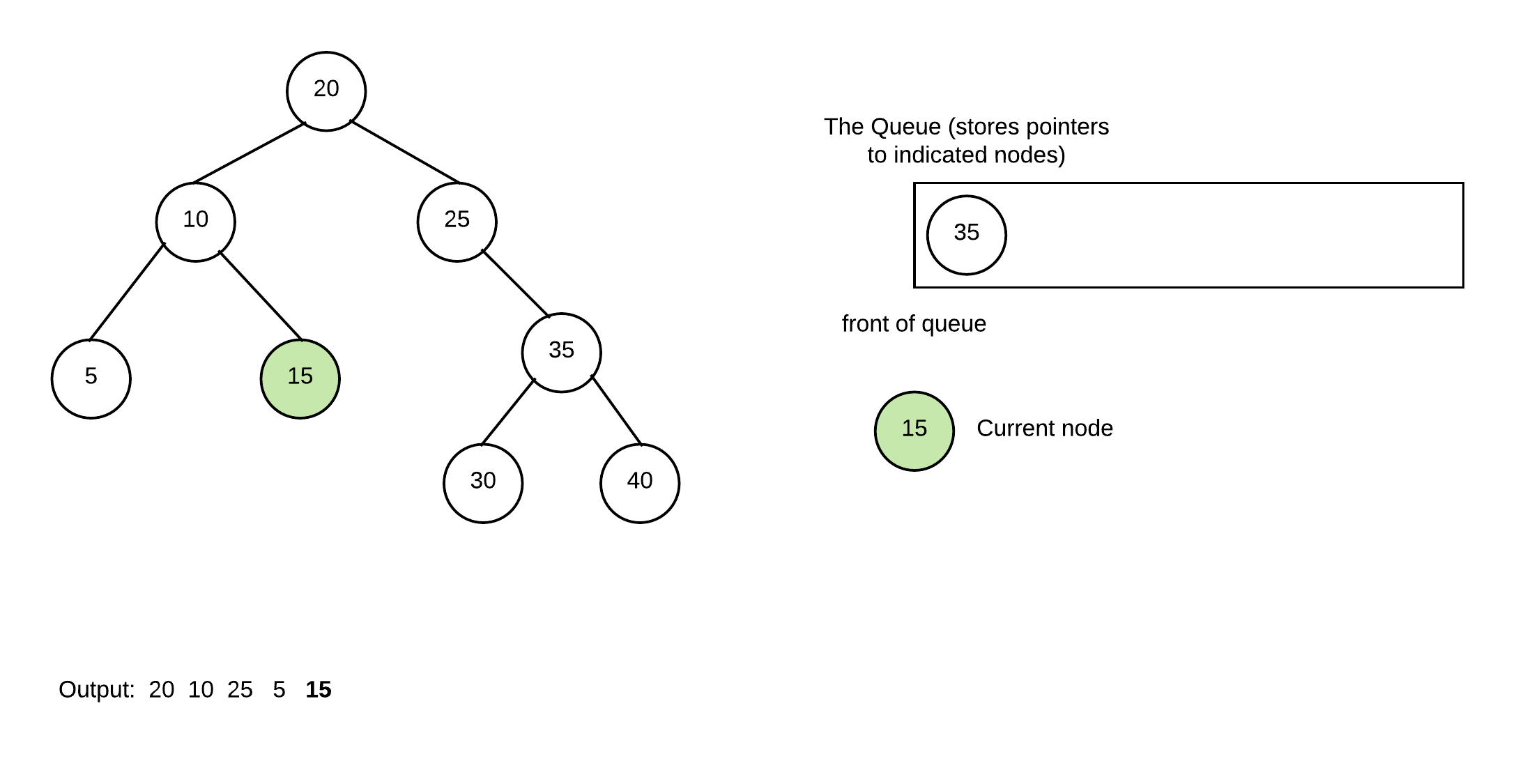
Repeat with 35 and add its children
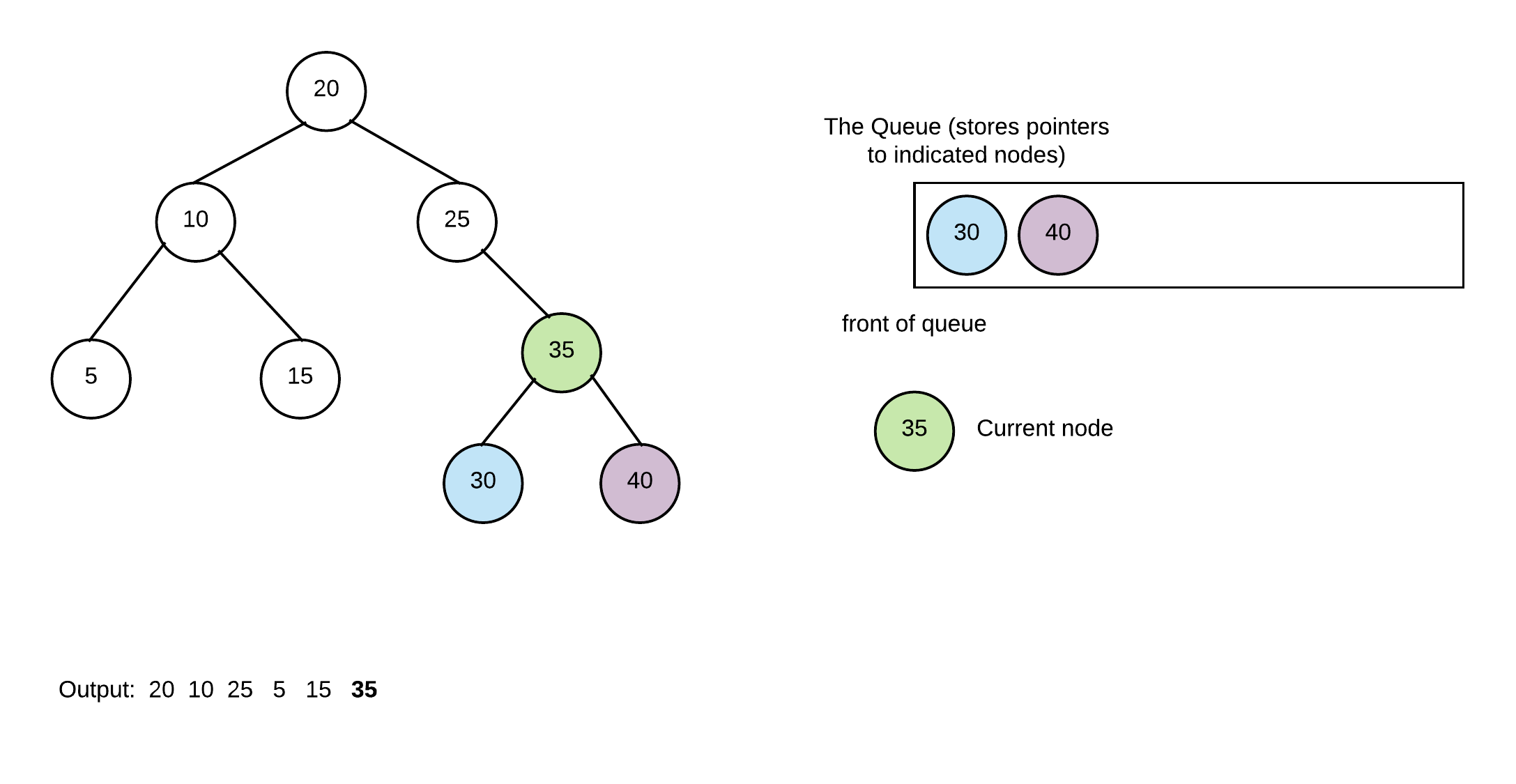
Continue by removing 30
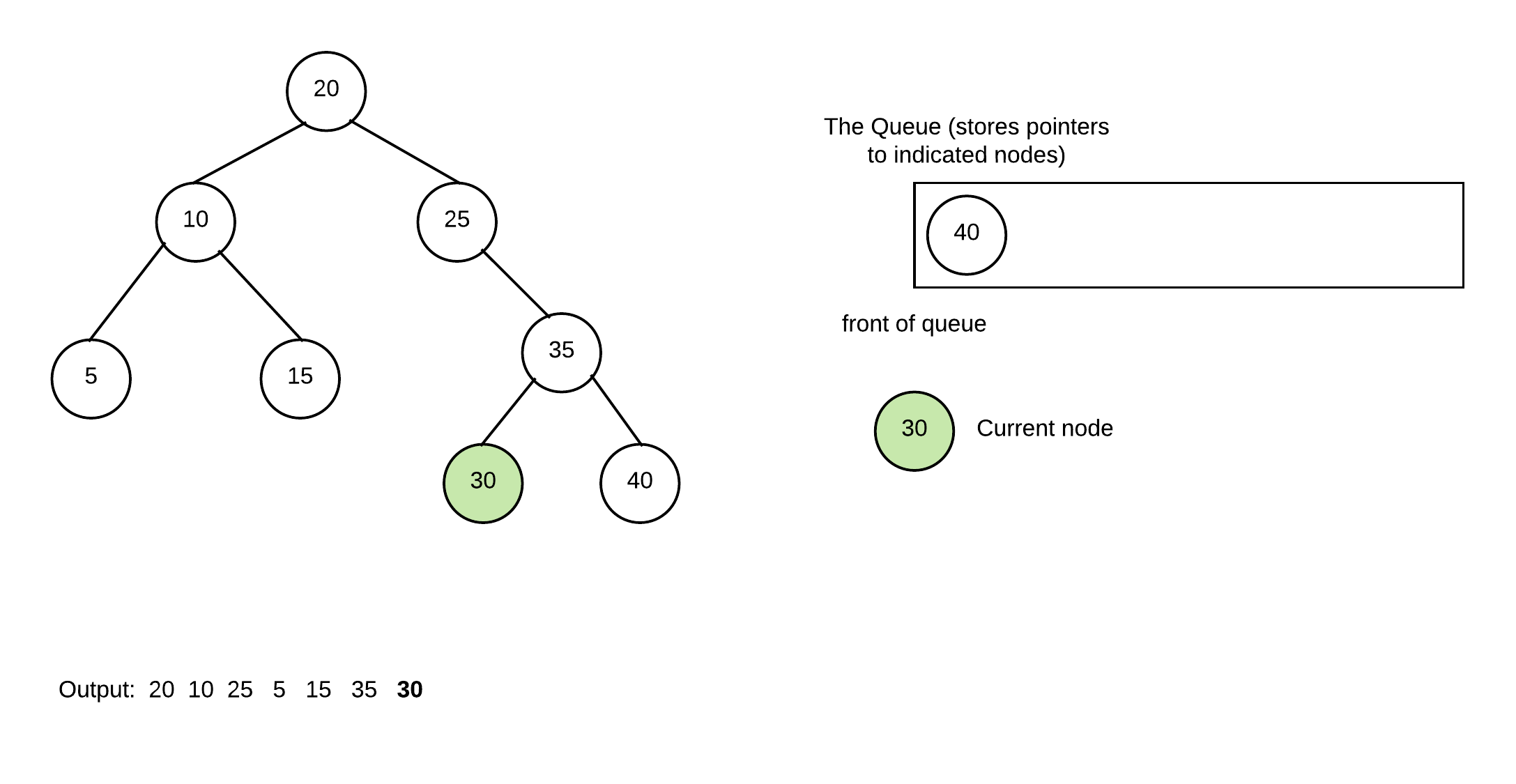
And one more time with 40
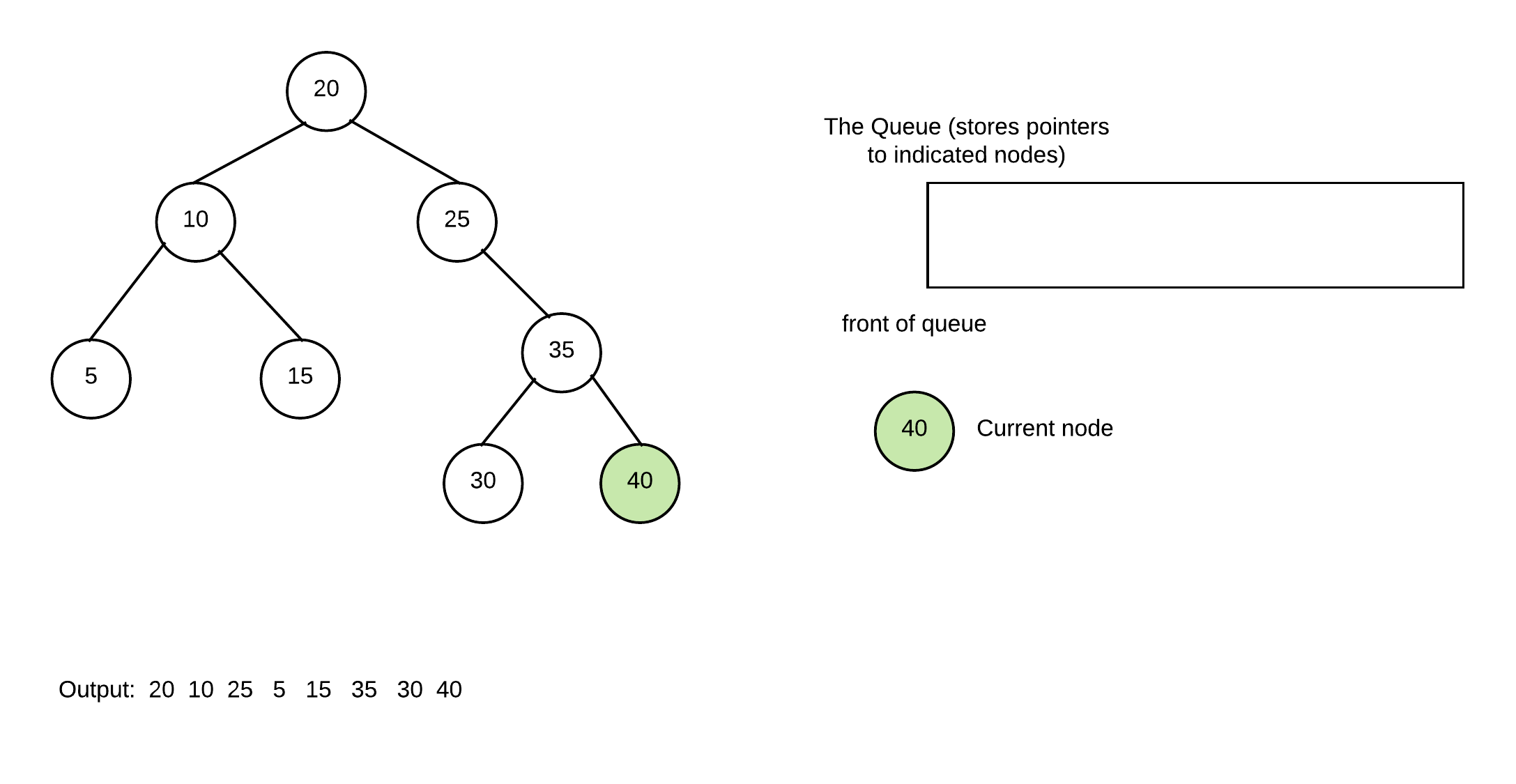
At this point queue is empty and thus, we have completed our breadthfirst print of the tree.
In code form, this is how we will write our code (we assume we have a template queue available:
- Python
- C++
import queue
class BST:
class Node:
# Node's init function
def __init__(self, data=None, left=None, right=None):
self.data = data
self.left = left
self.right = right
# BST's init function
def __init__(self):
self.root = None
def breadth_first_print(self):
the_nodes = queue.Queue()
if self.root is not None:
the_nodes.put(self.root)
while not the_nodes.empty():
curr = the_nodes.get()
if curr.left:
the_nodes.put(curr.left)
if curr.right:
the_nodes.put(curr.right)
print(curr.data, end=" ")
template <typename T>
class BST{
struct Node{
T data_;
Node* left_;
Node* right_;
Node(const T& data, Node* left=nullptr, Node* right=nullptr){
data_=data;
left_=left;
right_=right;
}
};
//single data member pointing to root of tree
Node* root_;
public:
...
void breadthFirstPrint() const{
Queue<Node*> theNodes; //we assume the queue class has these functions
//enqueue(), dequeue(), front(), isEmpty()
//prime queue
if(root_){
theNodes.enqueue(root_);
}
//while we have nodes to deal with
while(!theNodes.isEmpty()){
//deal with first node and remove it from queue
Node* curr=theNodes.front();
theNodes.dequeue();
if(curr->left_){
//if the current node has a left child add it to queue
theNodes.enqueue(curr->left_);
}
if(curr->right_){
//if the current node has a right child add it to queue
theNodes.enqueue(curr->right_);
}
//print the current node's data
std::cout << curr->data_ << " ";
}
std::cout << std::endl;
}
...
};