Example 1: Analysis of Linear Search

To look at how to perform analysis, we will start with a performance analysis of the following C++ function for a linear search:

Python

def linear_search(my_list, key):
    for i in range(0, len(my_list)):
        if my_list[i] == key:
            return i

    return -1

C++

template <class TYPE>
int linearSearch(const vector<TYPE>& arr, const TYPE& key){
    int rc=-1;
    for(int i=0;i<arr.size()&& rc==-1;i++){
        if(arr[i]==key){
            rc=i;
        }
    }
    return rc;
}

Assumptions

Looking at the C++ code (the Python one has been described a bit differently but has similar functionality,) we can see that there is a loop. The loop stops on one of two conditions, it reaches the end of the array or rc becomes something other than -1. rc changes only if key is found in the array. So, what are the possibilities when I run this program?

1) key is not in the array... in that case loop stops when it gets to the end of the array

2) key is in the array... but where? If it is at the front, then loop stops right away, if it is in the back then it needs to go through all the elements... clearly these will both affect how many operations we carry out.

The worst case scenario is that of an unsuccessful search... the loop will need to run more times for that. If the search was successful however, where will the key be? To perform an average case scenario, we need to consider the likelihood of finding the key in each element. Now, making the assumption that the key is equally likely to be in any element of the array, we should expect to go through half the array on average to find key.

We will look at each of these in turn below

Analysis of an Unsuccessful Search

Let n represent the size of the array arr.
Let T(n) represent the number of operations necessary to perform linear search on an array of n items.

Next we go through the code and count how many operations are done. We can do this by simply adding a comment to each line with the total operation count per line. That is we count how many operations are on that line AND the number of times that particularly line is done.

Python

def linear_search(my_list, key):
    for i in range(0, len(my_list)):     # n + 2
        if my_list[i] == key:            # n
            return i                     # 0

    return -1                            # 1

caution

In python3, range() and len() are both constant. Further, range() calls are done only once to determine the range() of values used for looping. This is not the same as testing the continuation condition in C/C++ which happens at top of every loop. Here, you loop through the entire range of values

Where do the counts come from?

• Firstly, n is the length of the list.

def linear_search(my_list, key):
    for i in range(0, len(my_list)):    # n + 2 - reason:  you change the value of i each time you go through loop.
                                        # This change is done for every value between from 0 to n-1 inclusive.
                                        # Thus, i is changed n times in total. len() function call is constant,
                                        # range() in python3 is also constant.  Thus, we count those items as 1
                                        # each.  range() is only called once to get all the values loop must
                                        # iterate through

        if my_list[i] == key:           # n - reason: every time in loop you must count the == (note operator, not
                                        # symbol.  == is the operator.  You require two equal signs to type it out,
                                        # but it is not two operators.  You can count [] as an op if you want
                                        # if you do it, do it consistently or not at all)

            return i                    # 0 - reason: on an unsuccessful search this return never occurs

    return -1                           # 1 - reason: on an unsuccessful search, this return always occurs

Come up with the expression for T(n)

Recall that T(n) represents the total number of operations needed for an unsuccessful linear search. As such, we get T(n) by summing up the number of operations. Thus:

$\begin{aligned} T(n) &= n + 2 + n + 1 \\ &= 2n + 3 \end{aligned}$

The $2n$ comes from the 2 operations that we do each time through the loop (note that we have n elements in the list/array.) The $+ 3$ comes from the 3 operations that we always have to do no matter what (the loop runs $n$ times and causes $2n + 2$ operations.)

Thus the expression for the number of operations that is performed is:

$T(n) = 2n + 3$

Now, imagine $n$ becoming a very very large number. As $n$ gets bigger and bigger, the $3$ matters less and less. Thus, in the end we only care about $2n$ . $2n$ is the dominating term of the polynomial. This is similar to this idea. If you had 2 dollars, then adding 3 dollars is a significant increase to the amount of money you have. However, if you had 2 million dollars, then 3 dollars matter very little. Similarly, in order to find something in an array with 2 million elements by comparing against each of them, doing just 3 ops we need to do to find the range, length of list, and return matters very little.

Using the dominating term, we can say that the linear search algorithm has a run time that never exceeds the curve for n. In other words, linear search is $O(n)$

Now... can we actually prove this?

According to the formal definition for big-O

" $T(n)$ is $O(f(n))$" if for some constants $c$ and $n_0$​​, $T(n) \leq cf(n)$ for all $n \geq n_0$

In other words... to prove that $T(n) = 2n + 3$ is $O(n)$ we must find 2 constants $c$ and $n_0$ ​​ such that the statement $T(n)\leq cn$ is true for all $n \geq n_0$

The important part about this... is to realize that we can pick any constant we want as long as it meets the criteria. For $c$ , I can pick any number > 2. I will pick 3 (there isn't a good reason for this other than 3>2), thus c = 3. I will also pick 3 for $n_0$. The reason is that starting at n == 3, $2n+3 \leq 3n$

We can see this in the graph below. Here, we see $T(n) = 2n +3$ (blue) as well as the $cf(n) = 3n$ (orange). At n==3, the line for $2n+3$ falls under $3n$ and it never gets above it again as n gets bigger and bigger

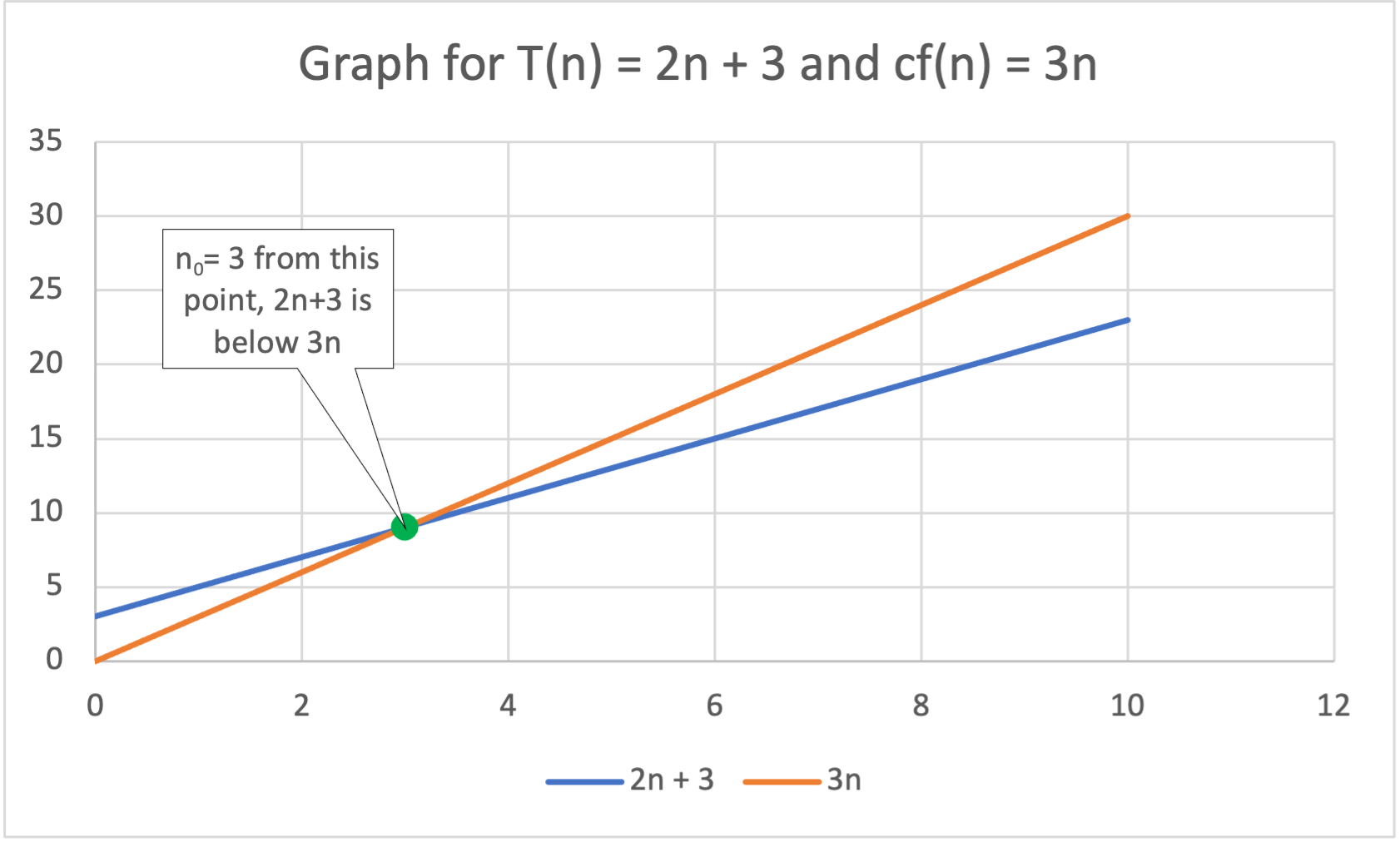
Thus, we have proven that the function is $O(n)$ because we were able to find the two constants $c$ and ​​ $n_0$ needed for the $T(n)$ to be $O(n)$

This is also the reason why it did not matter if we counted the [i] operator. If we counted that operator, our function would be : $T(n) = 3n + 3$.

The dominating term would be 3n. We would need to pick a different c that is greater than 3 and a different $n_0$ but we would still be able to find these and thus, T(n) is still O(n).

Analysis of a Successful Search

In the previous analysis, we assumed we wouldn't find the data and thus the worst possible case of searching through the entire array was used to do the analysis. However, what if the item was in the array?

Assuming that key is equally likely to be in any element, we would have to search through $n$ elements at worst (finding it at the last element) and $n \over 2​$ ​​ elements on average.

Now since we will at some point find the item, the statement inside the if will also be performed while the return -1 will not.

If we assume that the worst case occurs and we do not find the item until we get to the last element our operation count would be:

def linear_search(my_list, key):
    for i in range(0, len(my_list)):    # n + 2
        if my_list[i] == key:           # n
            return i                    # 1

    return -1                           # 0

When we add up our counts, we would end up with the same function.

If we assume we will only search half the list.. then what would we get?

def linear_search(my_list, key):
    for i in range(0, len(my_list)):    # n/2 + 2
        if my_list[i] == key:           # n/2
            return i                    # 1

    return -1                           # 0

T(n) = n/2 + 2 + n/2 + 1 = n + 3

In this case, the dominating term is n. and thus T(n) is still O(n)

C++

template <class TYPE>
int linearSearch(const vector<TYPE>& arr, const TYPE& key){
    int rc=-1;                                //1
    for(int i=0;i<arr.size()&& rc==-1;i++){   //1 + 5n
        if(arr[i]==key){                      //n
            rc=i;                             //0
        }
    }
    return rc;                                //1
}

caution

In the above code we are treating arr.size() function call as if its a constant value or variable. This can be done only because the size() function in vector class is constant. You can check this out here: https://en.cppreference.com/w/cpp/container/vector/size under the heading complexity. If the complexity was something else, we would need to account for this in the analysis. For example, strlen() in cstring library does not have a constant run time and thus we can't count it as one operation

Where do the counts come from?

• int rc=-1; is only ever done once per function call, there is one operator on that line, so the count is 1
• for(int i=0;i<arr.size()&& rc==-1;i++) int i=0 is only done once per function call, so it is counted as 1, the other operations <, . (dot), &&, == and ++ happen for each loop iterations and since the loop happens n times, each of those 5 operations are multiplied by n
• if(arr[i]==key) this is done every time we are in loop, loop runs n times, so count as 1
• rc=i it is worth noting that because we are assuming our search is unsuccessful, the if statement never evaluates to true, thus, this line of code never runs. Thus, it is not counted
• return rc; like the first initialization statement this return statement only happens once, so we count it as 1

Come up with the expression for T(n)

Recall that T(n) represents the total number of operations needed for an unsuccessful linear search. As such, we get T(n) by summing up the number of operations. Thus:

$\begin{aligned} T(n) &= 1 + 1 + 5n + n + 1 \\ &= 6n + 3 \end{aligned}$

The $6n$ comes from the 6 operations that we do each time through the loop. We have n elements in the array. Thus, the loop must run $6n$ times.

The $+ 3$ comes from the 3 operations that we always have to do no matter what.

Thus the expression for the nu-mber of operations that is performed is:

$T(n) = 6n + 3$

Now, imagine $n$ becoming a very very large number. As $n$ gets bigger and bigger, the $3$ matters less and less. Thus, in the end we only care about $6n$ . $6n$ is the dominating term of the polynomial. This is similar to this idea. If you had 6 dollars, then adding 3 dollars is a significant increase to the amount of money you have. However, if you had 6 million dollars, then 3 dollars matter very little. Similarly if you had to find something in an array with 6 million elements

Using the dominating term, we can say that the linear search algorithm has a run time that never exceeds the curve for n. In other words, linear search is $O(n)$

Now... can we actually prove this?

According to the formal definition for big-O

" $T(n)$ is $O(f(n))$" if for some constants $c$ and $n_0$​​, $T(n) \leq cf(n)$ for all $n \geq n_0$

In other words... to prove that $T(n) = 6n + 3$ is $O(n)$ we must find 2 constants $c$ and $n_0$ ​​ such that the statement $T(n)\leq cn$ is true for all $n \geq n_0$

The important part about this... is to realize that we can pick any constant we want as long as it meets the criteria. For $c$ , I can pick any number > 6. I will pick 10 (there isn't a good reason for this other than its bigger than 6, and the math is easy to do in our head for the purposes of presenting this) c = 10. I will also pick 1 for $n_0$ ​​,

The following graph shows both $T(n) = 6n +3$ (blue) as well as the $cf(n) = 10n$ (orange). At some point, the line for $6n+3$ falls under $10n$ and it never gets above it after that point.

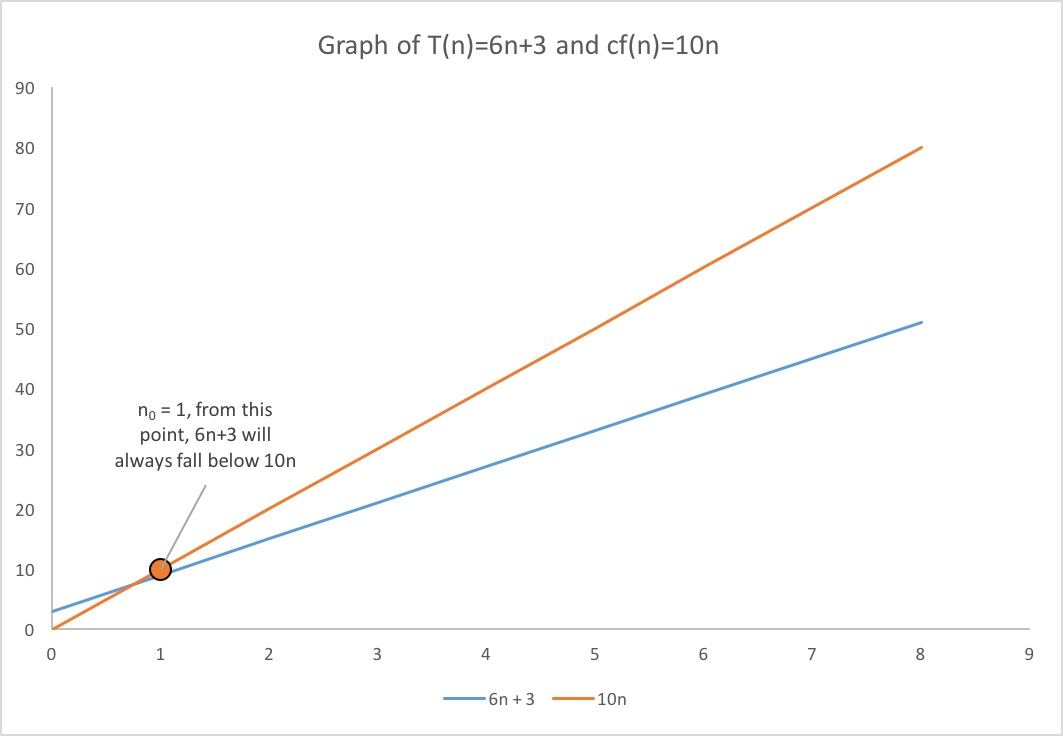
Thus, we have proven that the function is $O(n)$ because we were able to find the two constants $c$ and ​​ $n_0$ needed for the $T(n)$ to be $O(n)$

This is also the reason why it did not matter if we counted the operations for the . operator or the [i] operator. If we counted both of them,

$T(n) = 8n + 3$

The dominating term would be 8n but this is still O(n).

The proof would go exactly the same way except that we can't use $n_0 = 1$ as the statement $T(n) \leq cn$ is not true when $n = 1$ . However, when $n = 2$ , $T(n) = 19$ and $cn$ would be 20. Thus, it would be true and stays true for all values of $n > 2$

Analysis of a Successful Search

In the previous analysis, we assumed we wouldn't find the data and thus the worst possible case of searching through the entire array was used to do the analysis. However, what if the item was in the array?

Assuming that key is equally likely to be in any element, we would have to search through $n$ elements at worst and $n \over 2​$ ​​ elements on average.

Now since we will at some point find the item, the statement inside the if will also be performed. Thus, we will have 4 operations that we must run through once.

int rc = -1
int i = 0
rc=i
return rc;

These other operations will also run for each iteration of the loop:

i<arr.size() && rc == -1   --> 3 operations
i++                        --> 1 operation
if(arr[i]==key)            --> 2 operations

The difference is we do not expect that the loop would have to run through the entire array. On average we can say that it will go through half of the array.

Thus:

$T(n) = 6 * 0.5 n + 4 = 3n + 4$

Now... as we said before... the constant of the dominating term does not actually matter. $3n$ is still $n$ . Our proof would go exactly as before for a search where the key would not found.

caution

One thing to note. If you flip between the python code and the C/C++ code, it would seem that the number steps is higher in the C/C++ version of the code. However, this does not mean that the C/C++ version of the code is slower. In fact generally speaking, you will find C/C++ code to run faster than python due to the way it is optimized and the way it runs. This is why any application where speed truly matters in real time is often written in C/C++. So you cannot compare the two in this manner! Algorithms analysis gives you performance only as a function of resource consumption. it does not translate directly into wall clock time!