Skip to main content

Graph Definition

The formal definition of a graph is as follows:

A Graph G=(V,E)G=(V,E) is made up made of a set of vertices V=v1,v2,v3...V={v_1, v_2, v_3...} and edges E=e1,e2,e3...E ={e_1,e_2, e_3...}. Each edge in EE defines a connection between (u,v)(u,v), where u,v∈Vu,v \in V

Basically this means that a graph is made up of vertices and edges. Each edge connects two of the vertices together. A graph is represented visually as follows:

Vertices​

A vertex in a graph represents some type of object. The full graph is about relationships between these objects. For example, suppose you wanted to represent the flights between various airports for an airline. the airports would each be represented by a vertex.

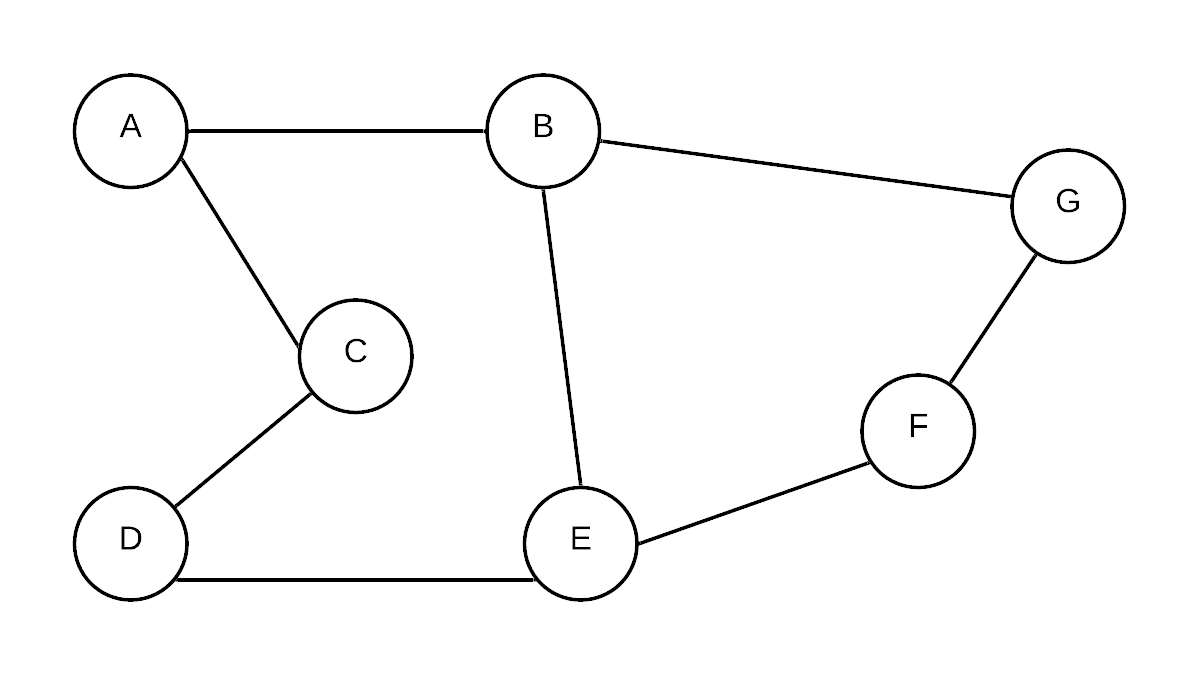
When we look at a graph, we typically label each vertex. For example:

This graph has vertices A, B, C, D, E, F and G. If we were to represent the objects involved with a specific problem, we would store information about each object into records and store them into a table.

::: info

Note that the vertex labels A,B,C etc. are just labels. These labels are used to refer to the vertices in the diagram... in reality we don't necessarily store/name labels in this manner. Often vertices are just identified by a number or has some other identifying feature.

:::

Edges​

Edges represent a connection between two vertices.

Aside from identifying a connection between vertices, edges can also have weights. For example:

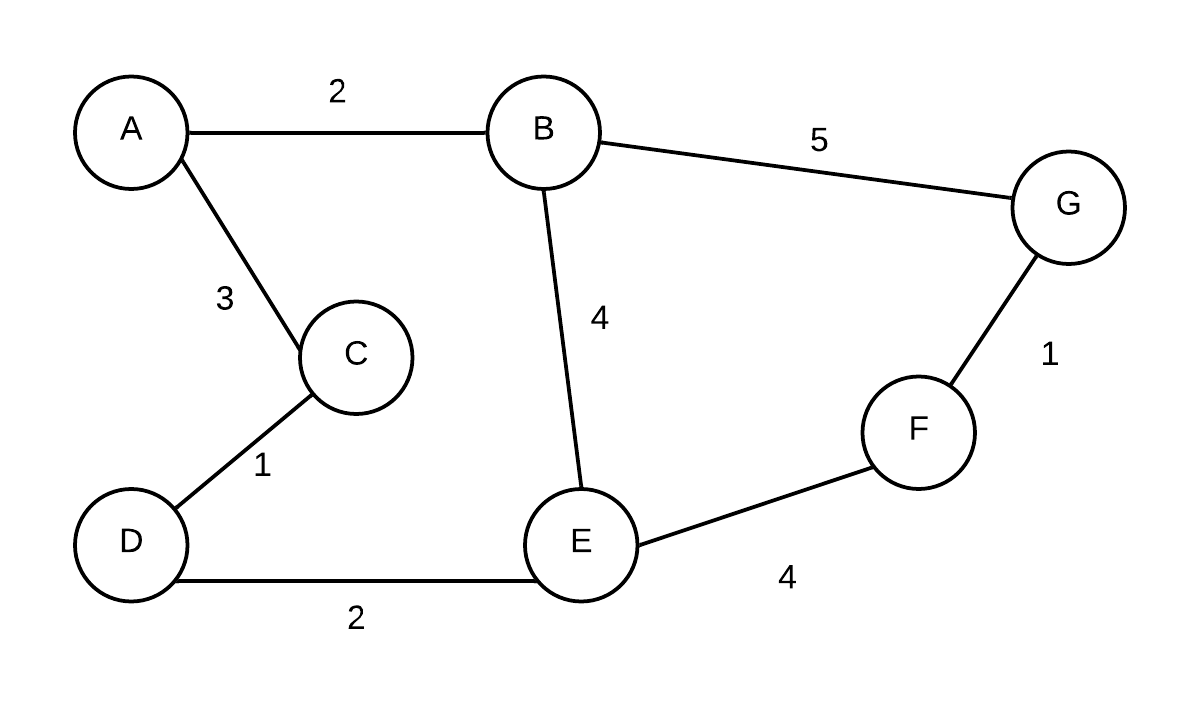
The weights on an edge can act in a way to serve as information about the nature of the connection between two vertices. For example, each vertex can represent a city and the weights, the distance between the cities.

Aside for weights, an edge may also include a direction. Graphs where edges have directions are also called a digraph. The following graph has both weights and direction:

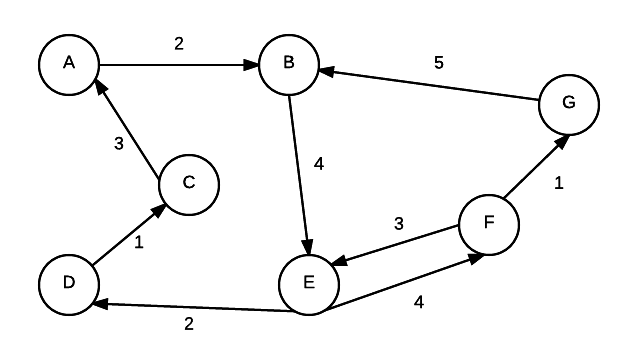
Other Definitions​

  • adjacent - Given two nodes A and B. B is adjacent to A if there is a connection from A to B. In a digraph if B is adjacent to A, it doesn't mean that A is automatically adjacent to B.
  • edge weight/edge cost - a value associated with a connection between two nodes
  • path - a ordered sequence of vertices where a connection must exist between consecutive pairs in the sequence.
  • simplepath - every vertex in path is distinct
  • path length - the number of the edges in a path.
  • cycle - a path where the starting and ending node is the same
  • strongly connected - If there exists some path from every vertex to every other vertex, the graph is strongly connected.
  • weakly connected - if we take away the direction of the edges and there exists a path from every node to every other node, the digraph is weakly connected.