Representation
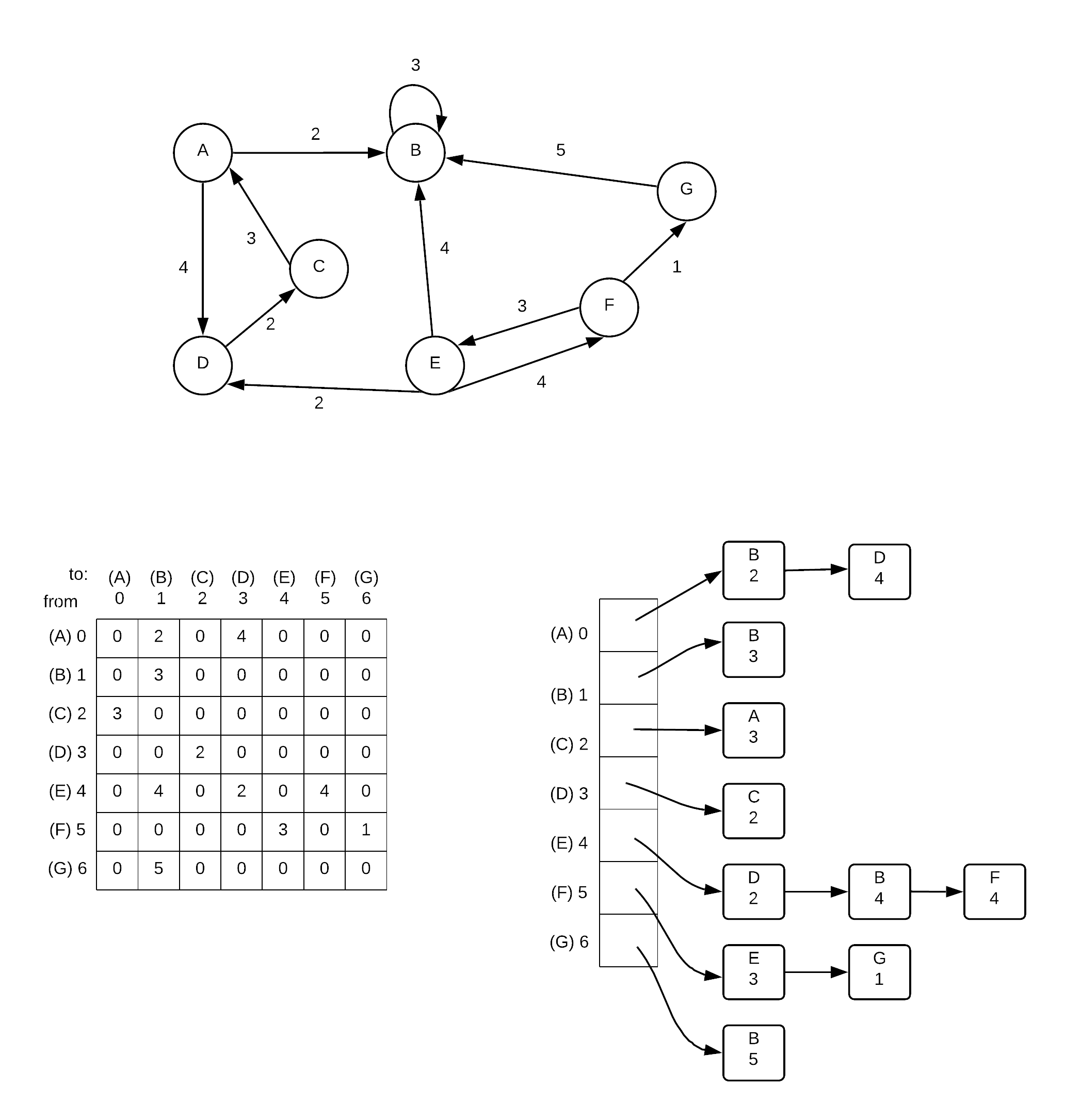
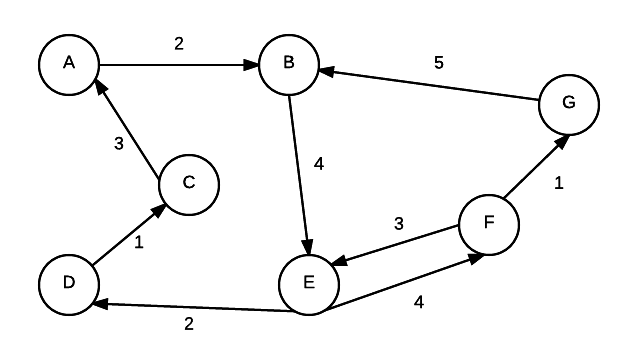
To store the info about a graph, there are two general approaches. We will use the following digraph in for examples in each of the following sections.
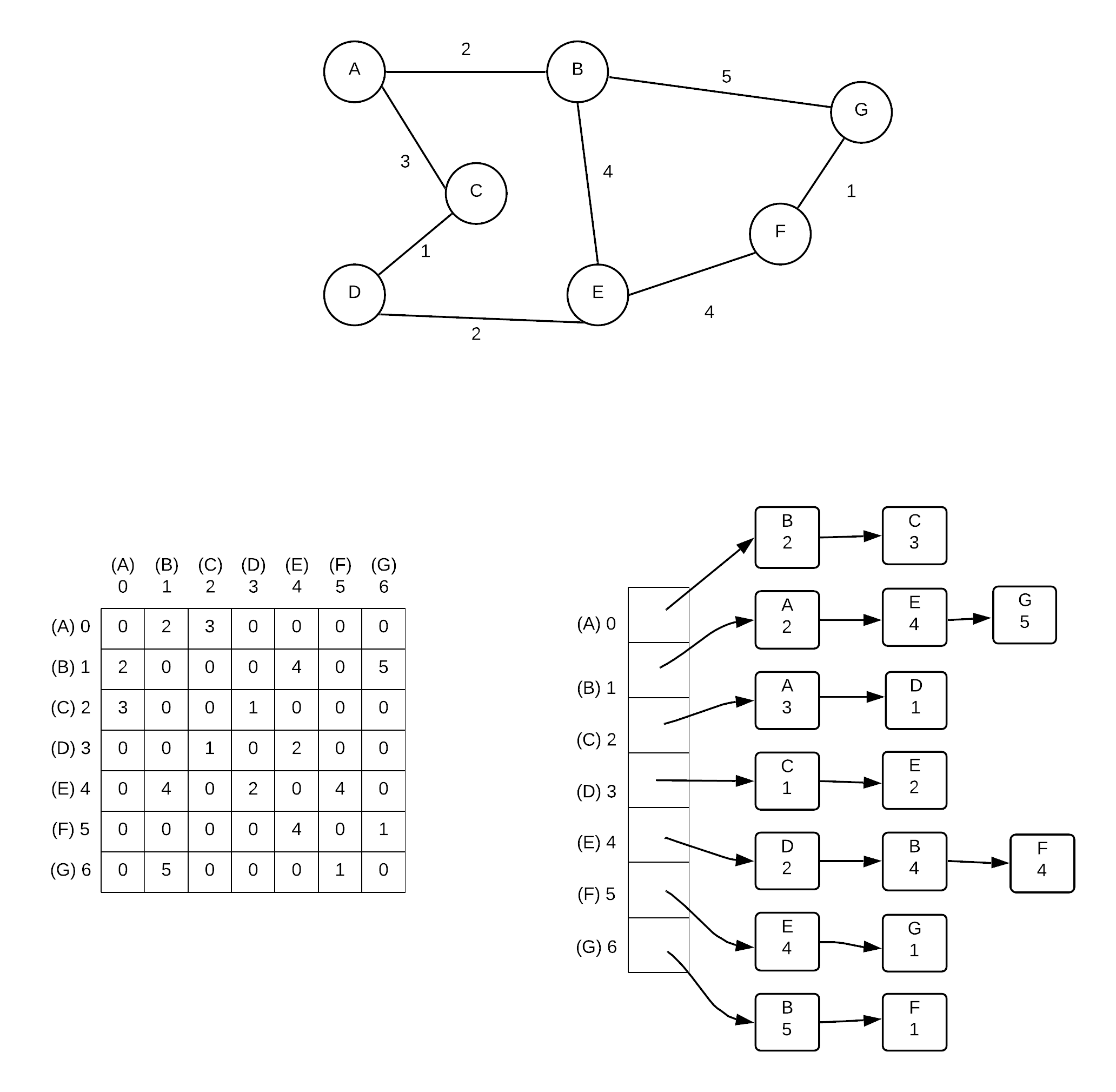
Adjacency Matrix
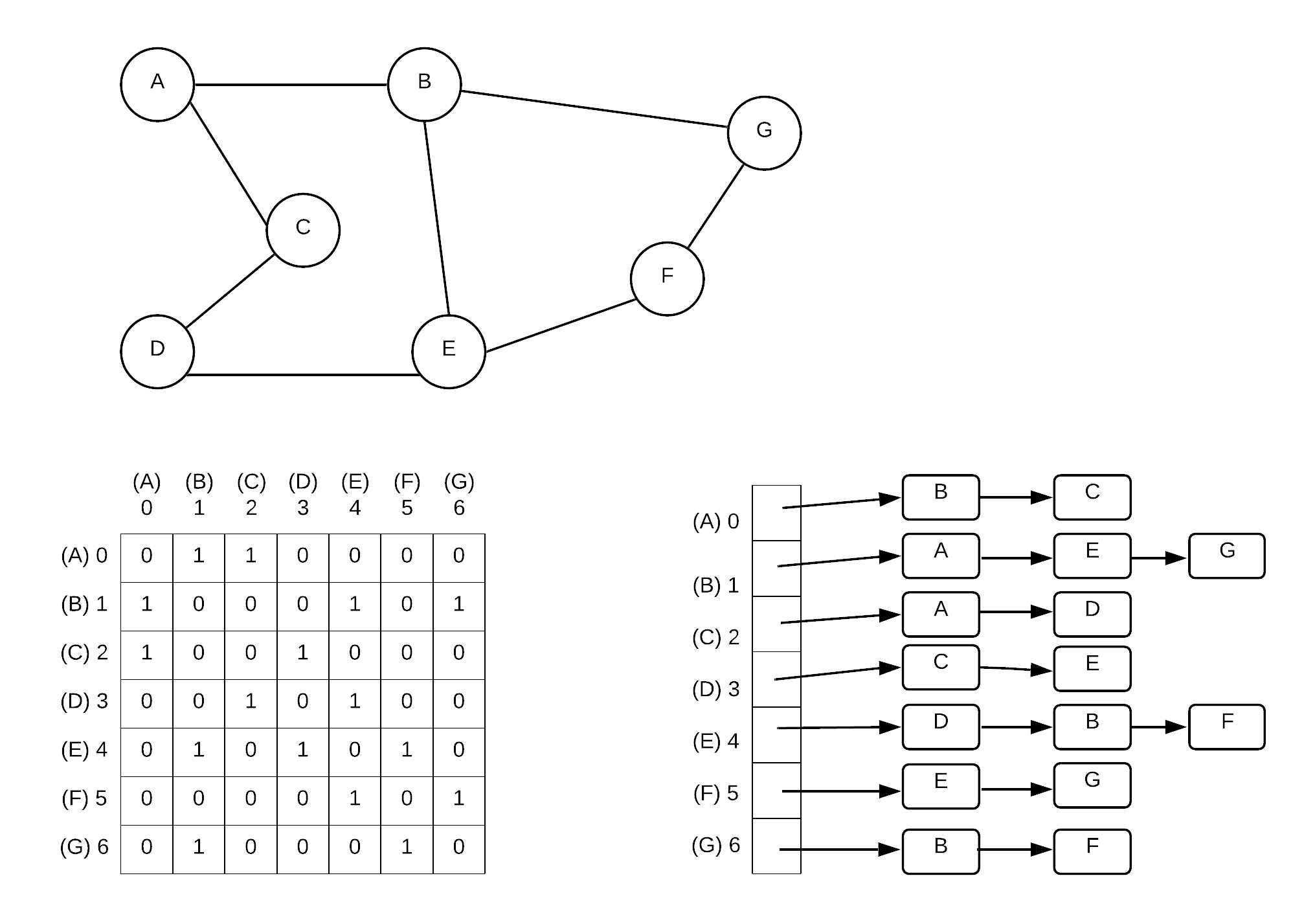
An adjacency matrix is in essence a 2 dimensional array. Each index value represents a node. When given 2 nodes, you can find out whether or not they are connected by simply checking if the value in corresponding array element is 0 or not. For graphs without weights, 1 represents a connection. 0 represents a non-connection.
The graph adjancey matrix is a good represenation if the graph is dense. It is not good if the graph is sparse as many of the values in the array will be 0.
An adjacency matrix representation can provide an O(1) run time response to the question of whether two given vertices are connected (just look up in table)
| A-0 | B-1 | C-2 | D-3 | E-4 | F-5 | G-6 | |
|---|---|---|---|---|---|---|---|
| A-0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 |
| B-1 | 0 | 0 | 0 | 0 | 4 | 0 | 0 |
| C-2 | 3 | 0 | 0 | 0 | 0 | 0 | 0 |
| D-3 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| E-4 | 0 | 0 | 0 | 2 | 0 | 4 | 0 |
| F-5 | 0 | 0 | 0 | 0 | 3 | 0 | 1 |
| G-6 | 0 | 5 | 0 | 0 | 0 | 0 | 0 |
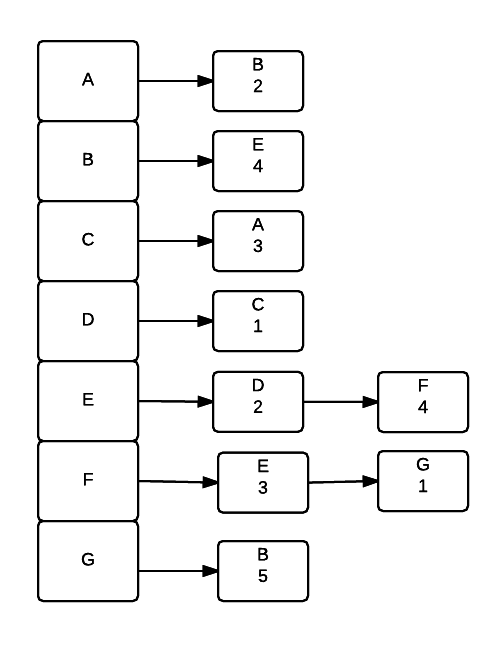
Adjacency List
An adjacency list uses an array of linked lists to represent a graph. Each element represents a vertex and for each (other) vertex it is connected to, a node is added to its linked list. For graphs with weights each node also stores the weight of the connection to the node. Adjacency lists are much better if the graph is sparse. It takes longer to answer the question of two given vertices are connected (Must go through list to check each node) but it can better answer the question given a single vertex, which vertices are directly reachable from that vertex.
Examples
A graph with no weights or directions
A graph with weights but no directions
A graph with weights and directions