Dijkstra's Algorithm
Dijkstra's Algorithm is an algorithm for finding the shortest path from one vertex to every other vertex. This algorithm is an example of a greedy algorithm. Greedy algorithms are algorithms that find a solution by picking the best solution encountered thus far and expand on the solution. Dijkstra's Algorithm was first conceived by Edsger W. Dijkstra.
The general algorithm can be described as follows:
- Start at the chosen vertex (we'll call it v1).
- Store the cost to travel to each vertex that can be reached directly from v1.
- Next look at the vertex that is least costly to reach from v1 (we'll call this vertex v2 for this example).
- For each vertex that is reachable from v2, find the total cost to that vertex starting from v1 (we want the total cost, not just the lowest cost from v2). Update the cost of travel to these vertices if it is lower than the current known cost.
- Pick the next lowest cost and continue.
Example
Consider the following graph (non-directed)
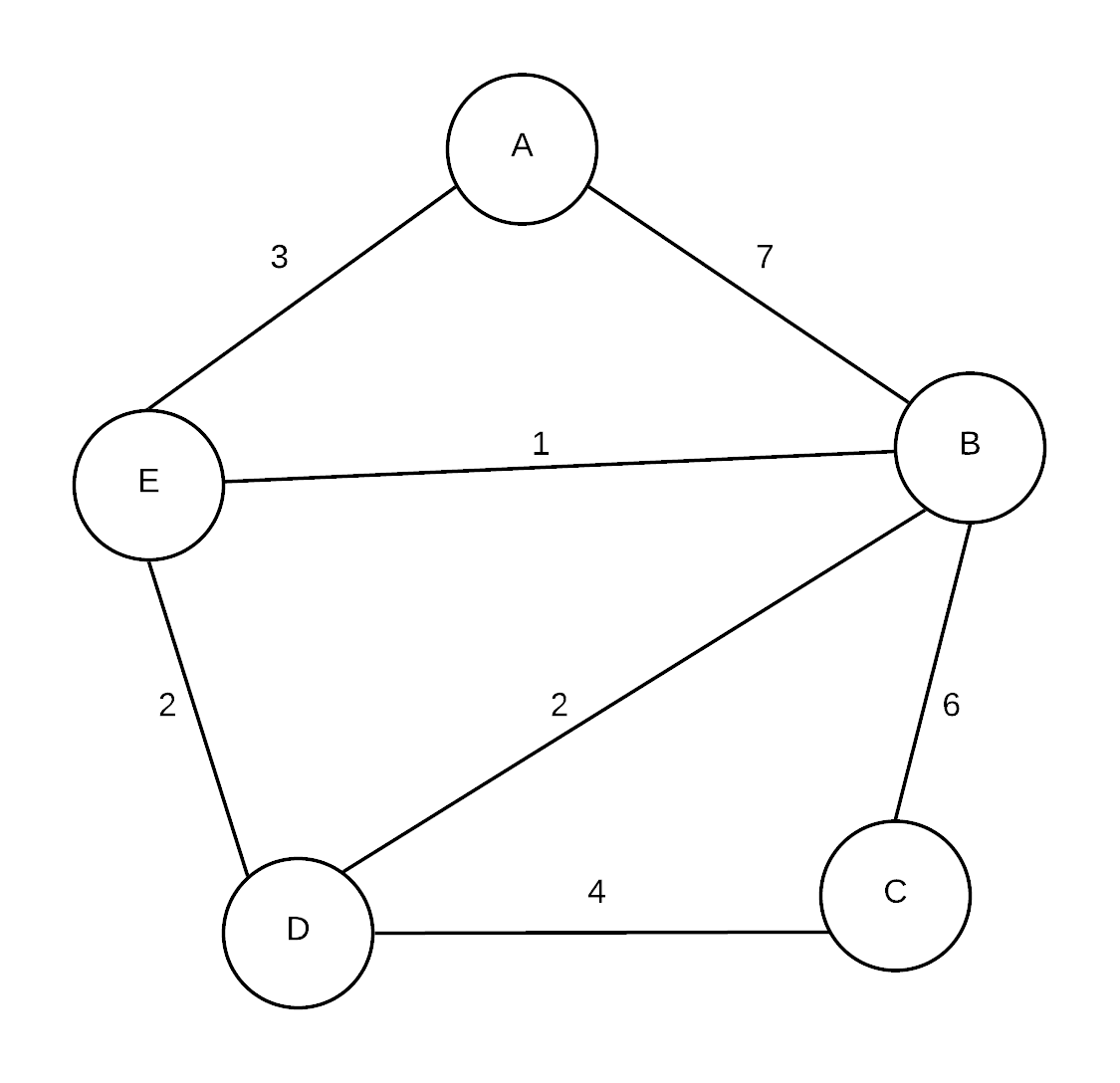
Initial state
We will use Dijkstra's algorithm to find the shortest distance from A to every other vertex. To track how we are doing, we will create a table that will track the shortest distances from A we have encountered so far as well as the "previous" node in the path (so if we follow all previous nodes, we end up back at A). We also track whether we "know" about the shortest path from A to each node... that is, have we already been able to find the shortest path to that node from A. Currently (at the beginning,) we do not know which nodes are reachable from A so we store infinity into every spot other than A. The cost of getting to A from A is 0. Initially the table looks like this:
| Vertex | Shortest Distance from A | Previous Vertex | Known |
|---|---|---|---|
| A | 0 | false | |
| B | false | ||
| C | false | ||
| D | false | ||
| E | false |
Expand A
Now, starting from A, there are two vertices that reachable, B and E
We store the total distance from A into the table for both these vertices if it is less than the shortest distance so far. At this point, A is now known as we have considered all its neighbours
| Vertex | Shortest Distance from A | Previous Vertex | Known |
|---|---|---|---|
| A | 0 | true | |
| B | A | false | |
| C | false | ||
| D | false | ||
| E | A | false |
Expand E
Now, we continue from here by considering the unknown vertex that has the shortest distance to A. In this case it is 3 (smallest in distance table with a false value in known). In implementation, we actually would use a priority queue (heap) to store the vertex with its distance and simply dequeue the smallest distance and check that the vertex was still unknown.
In any case, we are going to now consider E. From E the unknown neighbours are B and D. The distance to D (from A) is 5 (3 + 2). The distance to B is 4 (3 + 1). Now, The value stored previously for D was so we replace that with 5. The distance to B was 7, so we replace that also. We also mark that E is now known
| Vertex | Shortest Distance from A | Previous Vertex | Known |
|---|---|---|---|
| A | 0 | true | |
| B | E | false | |
| C | false | ||
| D | E | false | |
| E | A | true |
Expand B
The next vertex we consider is the one with the shortest distance to A that is still not known. This is now B.
From B, we can reach unknown neighbours C and D. The distance to C (from A) is 10 (4+6). The distance to D (from A) is 6 (4 + 2). The value stored in the table for C was so we replace that. The value stored in D was 5, so that entry is not replaced because this new distance is NOT smaller.
| Vertex | Shortest Distance from A | Previous Vertex | Known |
|---|---|---|---|
| A | 0 | true | |
| B | E | true | |
| C | B | false | |
| D | E | false | |
| E | A | true |
Expand D
The next vertex that with the smallest distance to A that is unknown is D. From D, there is only one unknown vertex (C). The distance to C is 9 (5 + 4). As this is smaller than what is stored, we will update the table
| Vertex | Shortest Distance from A | Previous Vertex | Known |
|---|---|---|---|
| A | 0 | true | |
| B | E | true | |
| C | D | false | |
| D | E | true | |
| E | A | true |
Expand C
The only vertex left is C. From C, there are no unknown neighbours so we mark C as known and we are done.
| Vertex | Shortest Distance from A | Previous Vertex | Known |
|---|---|---|---|
| A | 0 | true | |
| B | E | true | |
| C | D | true | |
| D | E | true | |
| E | A | true |
Shortest path
To find the shortest distance to A, we simply need to look it up in the final table.
However, if we want to find the shortest path it isn't so simple as a look up. We actually need to work away backwards by looking up the previous vertices. For example, to find shortest path from A to C, we see that C's previous was D. D's previous was E. E's previous was A. Thus, the path is:
A --> E --> D --> C