AVL Trees

An AVL tree creates and maintains a height balanced binary search tree. A height balanced tree is either empty or the height of the left and right subtrees differ by no more than 1. A height balanced tree is at most 44% taller than a perfectly balanced tree and thus, a search through a height balanced tree is O(log n). Insert and delete can also be done in O(log n) time.

Height Balance

AVL trees work by ensuring that the tree is height balanced after an operation. It does this by storing the height of every subtree in it's root. The storing of this height is the augmentation... we add this extra bit of info to every node and ensure its correctness after each operation that might modify a tree. We can then use this information to ensure that our tree is height balanced. By knowing how tall each subtree is, we can tell whether or not any subtree is too tall by calculating the balance from the height.

The balance of any node is calculated as:

Node's balance = height of right - height of left
     of node      subtree             subtree

When a tree is height balanced the balance of every node is either -1, 0 or +1

In an AVL tree, whenever we do any operation that may modify the tree, we ensure that no node's balance ends up as anything other than -1, 0 or +1.

Note that storing of the height in each node is essential. We cannot calculate the height as finding the height of a tree with n nodes is O(n)

The height balance of a node is calculated as follows:

Height Balance Implication

Recall that the following is the node's balance formula:

Node's balance = height of right - height of left
    of node      subtree             subtree

The above formula means that if the right subtree is taller, the height balance of the node will be positive. If the left subtree is taller, the balance of the node will be negative.

Insertion

Insertion in AVL tree is starts out similar to regular binary search trees. That is we do the following:

• Find the appropriate empty subtree where new value should go by comparing with values in the tree.
• Create a new node at that empty subtree.
• New node is a leaf and thus will have a height balance of 0
• go back to the parent and adjust the height balance.
• If the height balance of a node is ever more than 1 or less than -1, the subtree at that node will have to go through a rotation in order to fix the height balance. The process continues until we are back to the root.
• NOTE: The adjustment must happen from the bottom up

Example

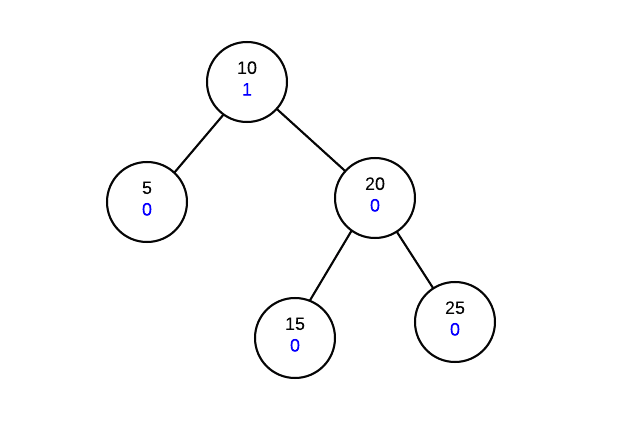
Suppose we have start with the following tree (value on top is the value, value on bottom is the height balance

Insert 30

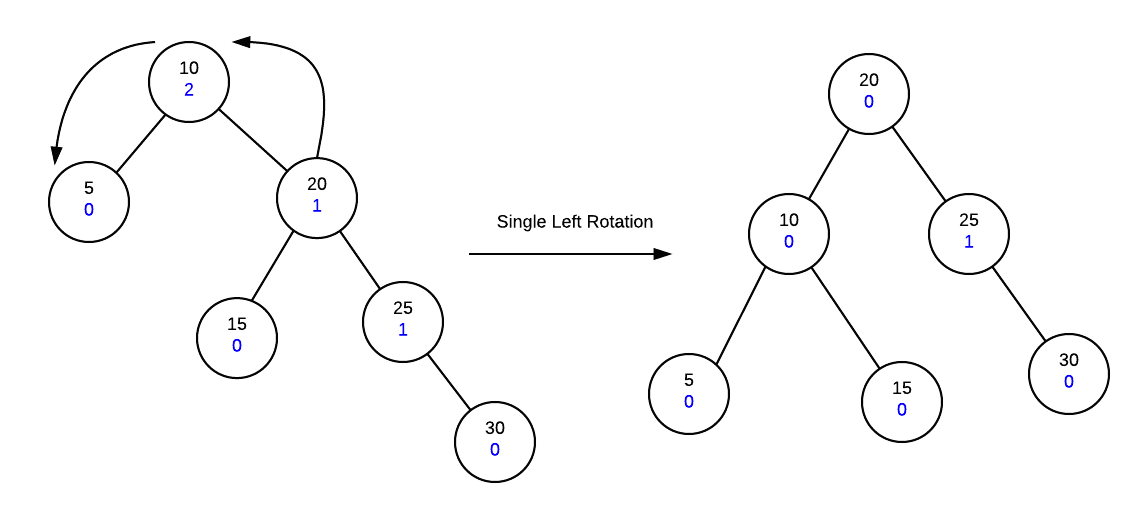
At this point, we have adjusted all the height balances along the insertion path and we note that the root node has a height balance of 2 which means the tree is not height balanced at the root.

In order to fix our tree, we will need to perform a rotation

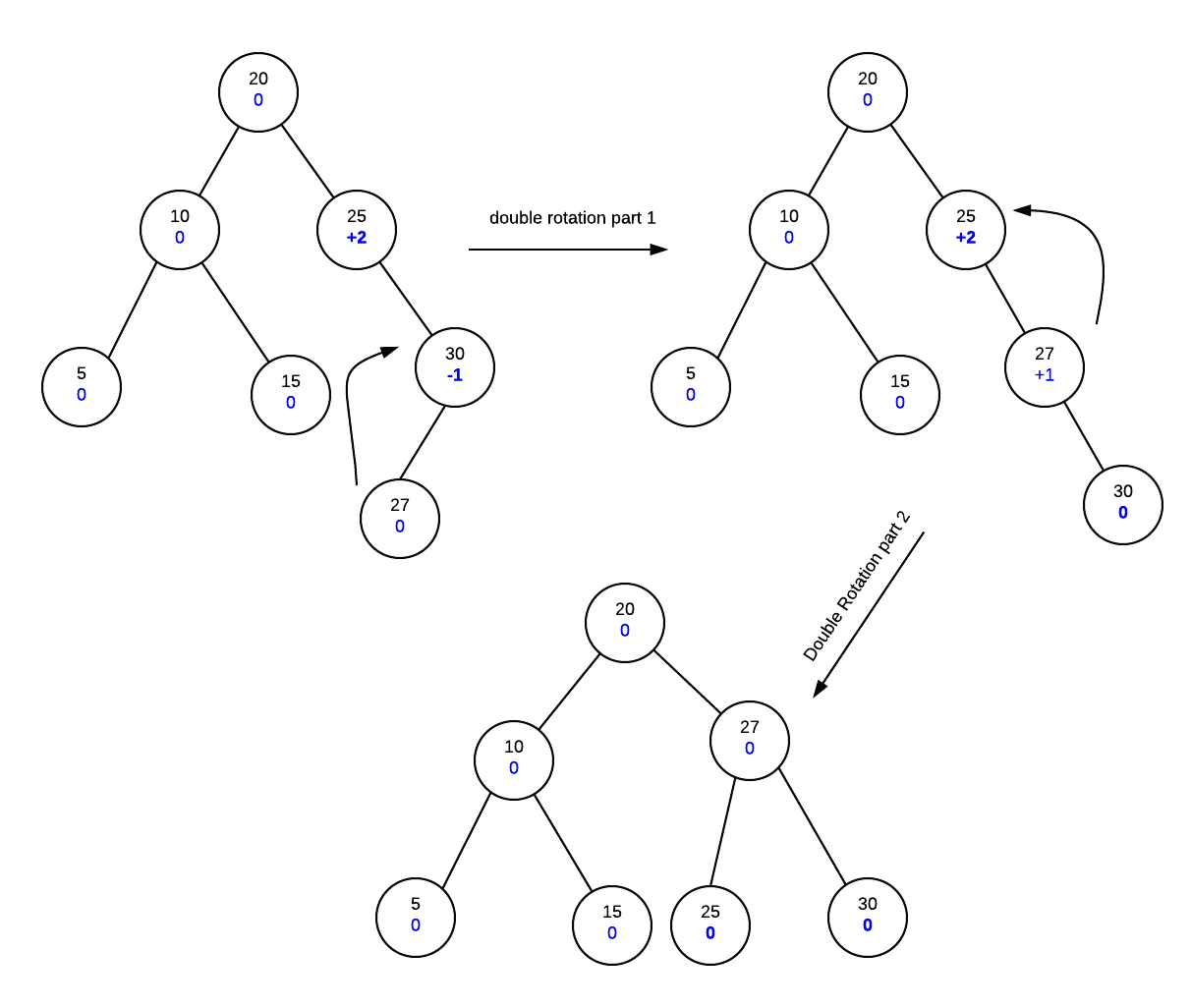
Insert 27

We start with our tree:

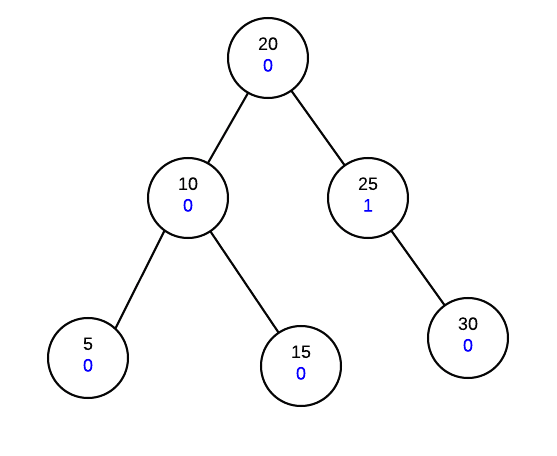
Now we find the correct place in the tree and insert the new node and fix the height balances

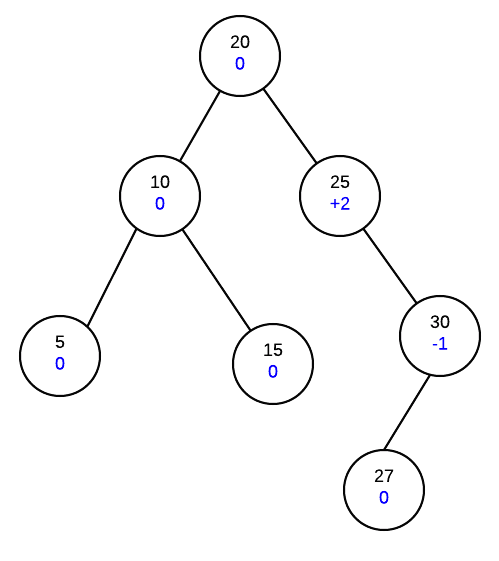
Now, as we reach node 25 and see that it the height balance is +2. If we then look at it's child's height balance we find that it is -1. As the signs are different, it indicates that we need a double rotation. Different signs indicate that the unbalance is in different directions so we need to do a rotation to make it the same direction then another to fix the unbalance.

Why does this work?

Single Rotation

We always fix nodes starting from the insertion point back to the root. Thus, any node in the insertion path further towards leaf nodes must already be fixed.

Consider the following idea of what an avl tree looks like:

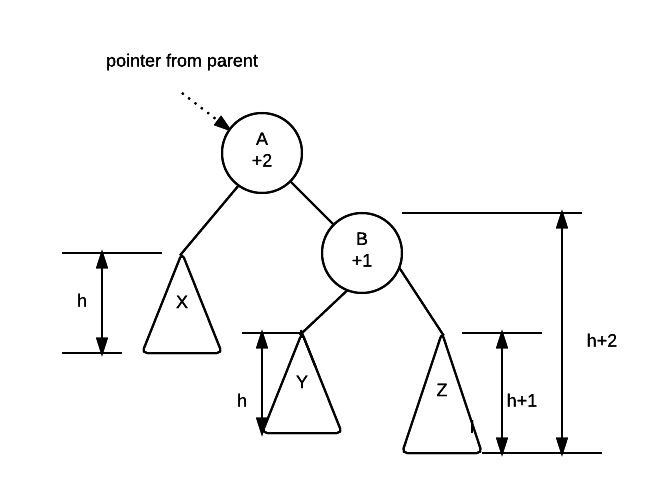
In this diagram, we have two nodes A and B and we see their height balance. We know that the subtrees X, Y and Z are valid avl trees because they would have been fixed as we process our tree back to the root.

From here we also know that:

all values  <  A  <  all values  <  B  <  all values
in X                     in Y                in Z

While we don't know how tall X, Y and Z are, we know their relative heights because we know the height balance.

Thus, if X has a height of h, B must be h+2 tall because the height balance at A is +2. This means that the right subtree at B is 2 taller than A.

Continuing on, we know that Z is the taller of the two subtrees of B because the height balance is +1, and thus Z must be h+1 tall while Y must be h tall.

A rotation repositions B as the root of the tree, makes node A the left child of B. Make Y the right child of A.

Given that X, Y and Z are unchanged, the height balance at A and B will become 0.

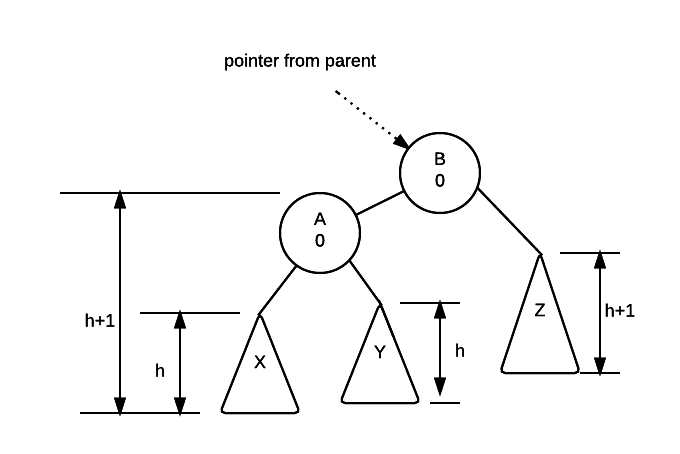
The mirror of the above is true for single left rotation

Double Rotations

A similar explanation of why double rotations work can be reasoned out by looking at the following tree:

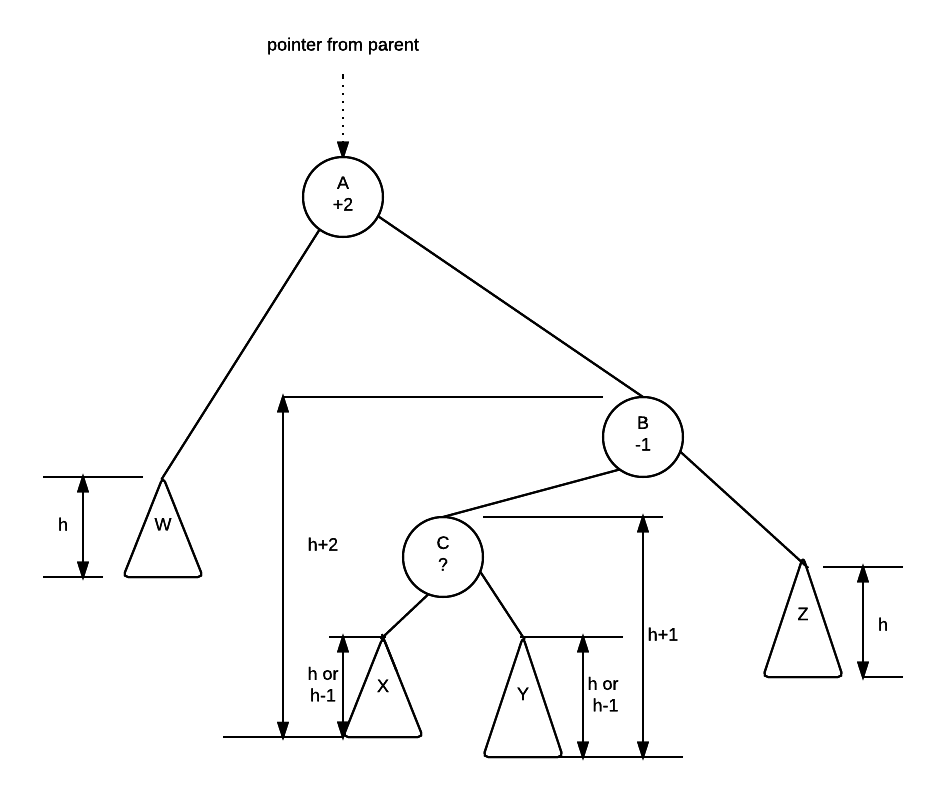
We know that W, X, Y and Z are all valid avl trees. We also know the following about the values in each of the trees and nodes

all              all               all          all
values  <  A  <  values  <  C  <  values < B <  values
in W              in X             in Y          in Z

Now... we know the height balance of A and B (off balance node and child) we do not know the exact height balance of C. However, we do know that it is a valid avl tree, so C's height balance must be either -1, 0 or +1.

So, if C's height balance is 0, then both x and y will have height of h.

if C's height balance is +1 then y will be h and x would be h-1

if C's height balance is -1 then x would be h and y would h-1

Perform a double rotation:

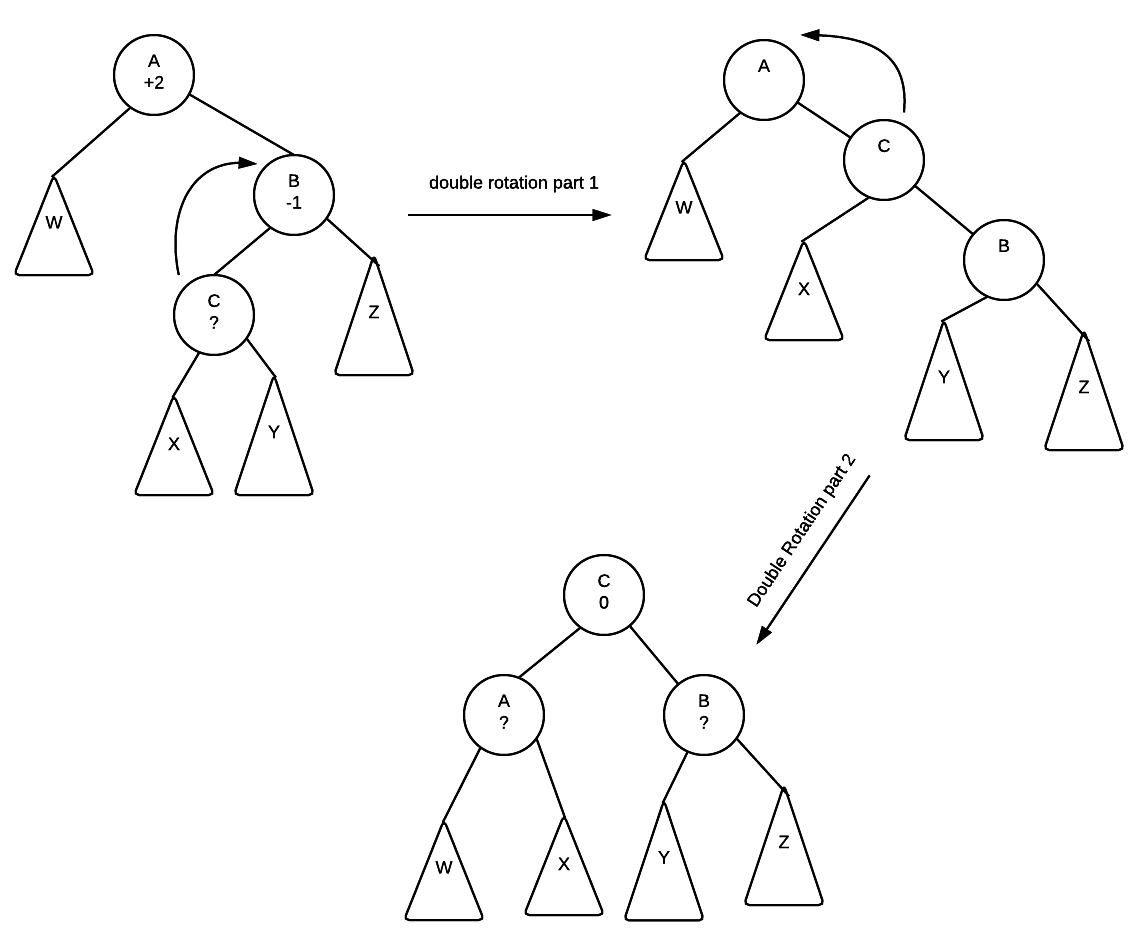
After the rotation is completed, notice that the position of the subtrees W,X, Y and Z along with the nodes A, B and C are placed in a way where their ordering is properly maintained.

Furthermore, The height balance of C becomes 0 regardless of what it was initially. The final height balance of A and B depends on what the original height balance of C was:

original height balance of C	height of X	height of Y	final height balance of A	final height balance of B
-1	h	h-1	0	+1
0	h	h	0	0
+1	h-1	h	-1	0

Deletion

The deletion algorithm for AVL trees must also keep the tree height balanced. This section will look at how deletion works.

The deletion algorithm does the following:

• In general follow BST deletion rules.
  • if node is leaf delete node, set pointer from parent to nullptr
  • if node has one child, have parent point to only child
  • if node has two children replace deleted node with inorder successor
• Because a deletion could potentially shorten a tree, we might need to adjust the tree. Starting with the deleted node (which may not actually be the node that contains the value we are getting rid of... more on this later) work our way back up to root, fix the height/balance info and rotate as needed.

The rest of this section will look at how it works

Deletion always removes a leaf node

Deletion always removes a leaf node. The previous statement may seem a bit odd because it seems like it can't be true, but it is. Note that node being remove isn't necessarily the node where value being removed was originally found. Lets consider the three deletion cases to explain why it is true:

Value is found in a leaf node

In this case, clearly the node to be removed is a leaf as we found it there. Thus, we get rid of it, adjust or height/balance values going back up the tree

Value is in a node with exactly one child

A node with only one child means that the only child is a leaf. The reason for this is because our tree is height balanced to start with. If the only child had a child, the node wouldn't have been height balanced as illustrated in the following diagram:

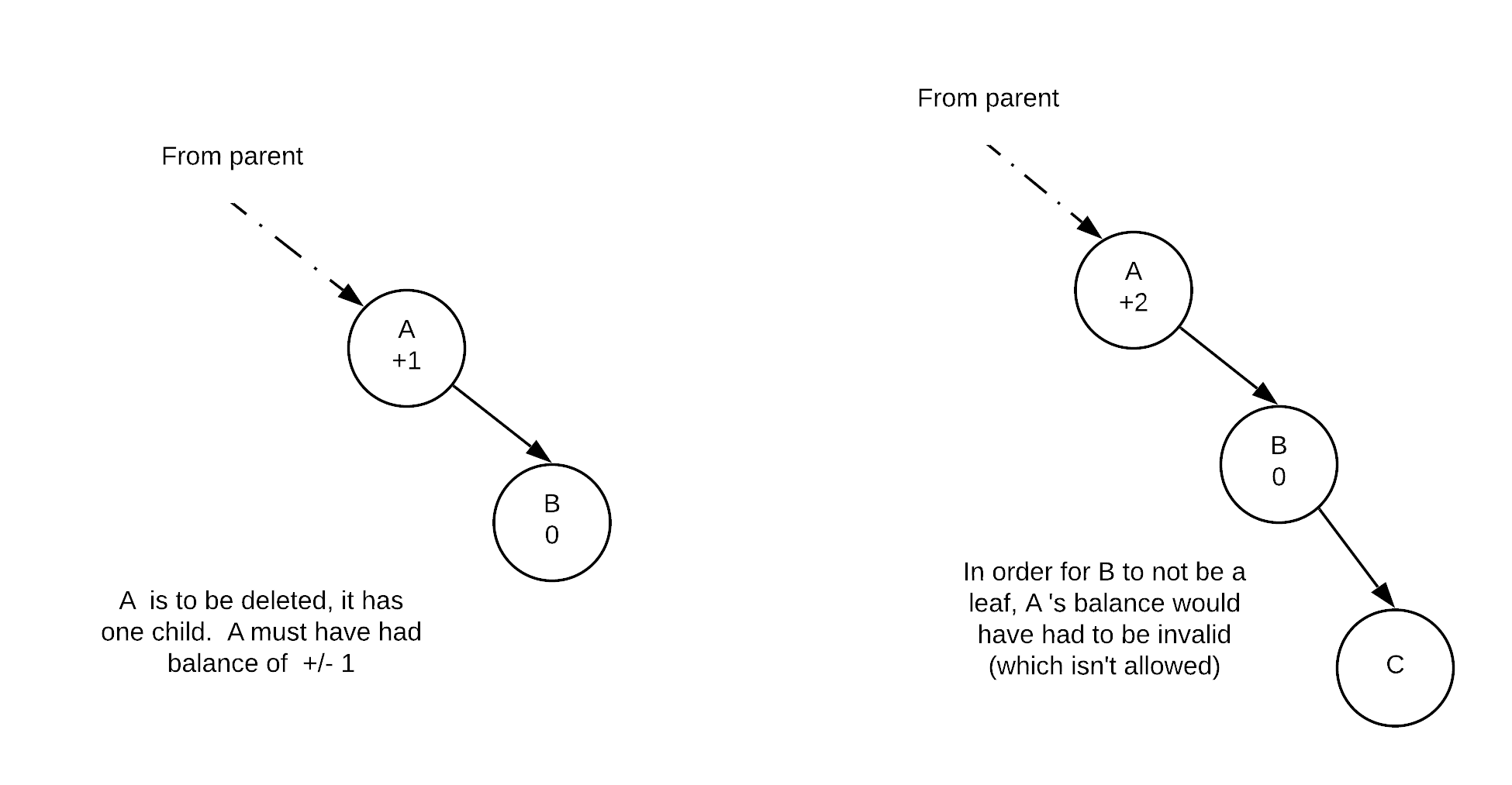
Thus, what effectively happens is that we end up with a tree that is shaped like we were removing B

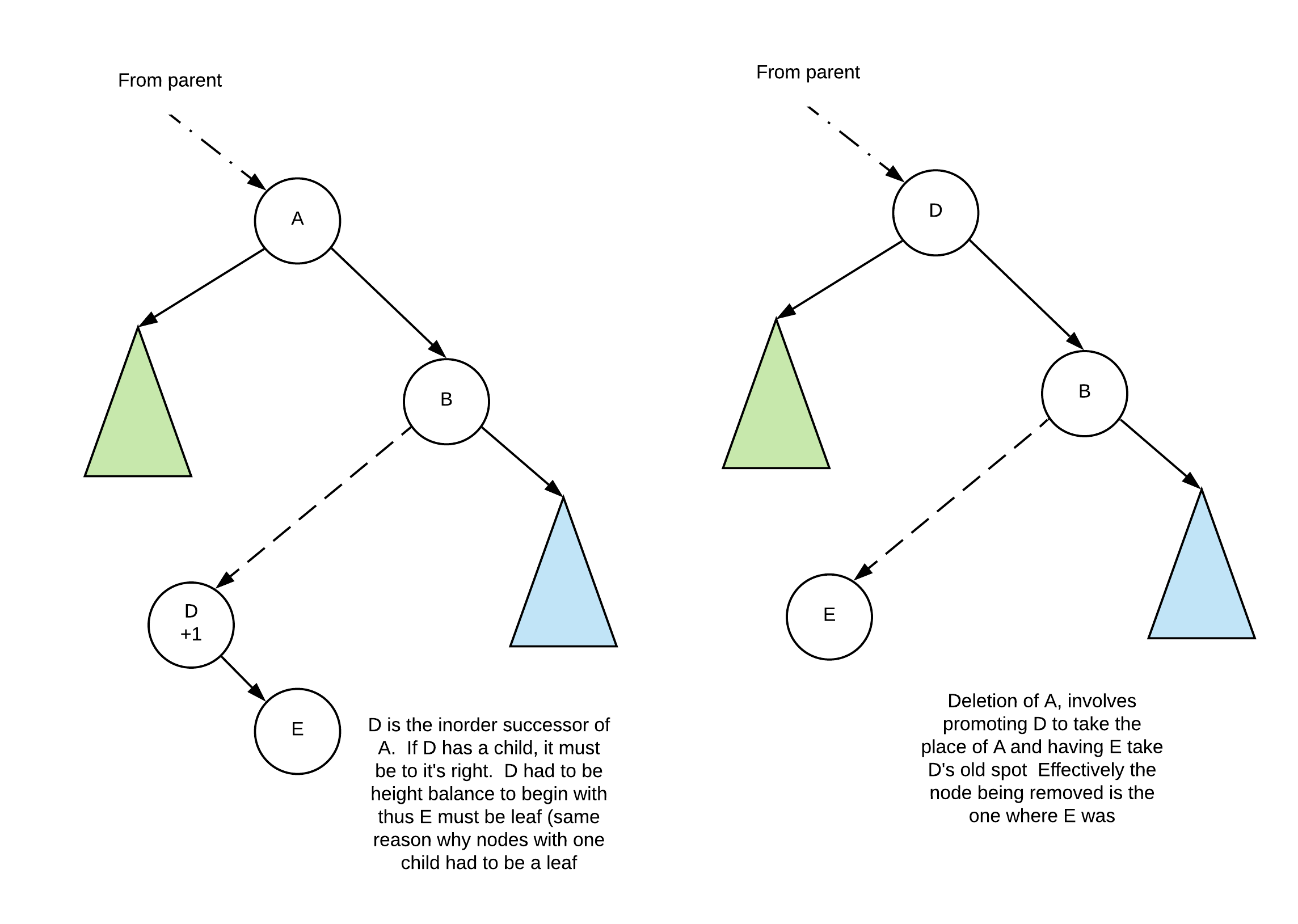
Value is in a node with exactly two children

The algorithm to remove a node with two children is to replace the node with its inorder successor node. This node is found by going one node to the right then going left until you can't. The inorder successor itself can only have a right child (if it had a left child it wouldn't be the inorder successor). As with the case of nodes with only one child, the inorder sucessor's right child must be a leaf because the inorder successor must have been height balanced before the deletion operation.

Fixing the tree

When will we need to fix the tree?

Clearly if the deletion doesn't shorten its subtree, there is nothing that needs to be done.

Thus, we only need to consider what happens if deleting the node causes the tree to shorten. In the examples below we only consider those situations.

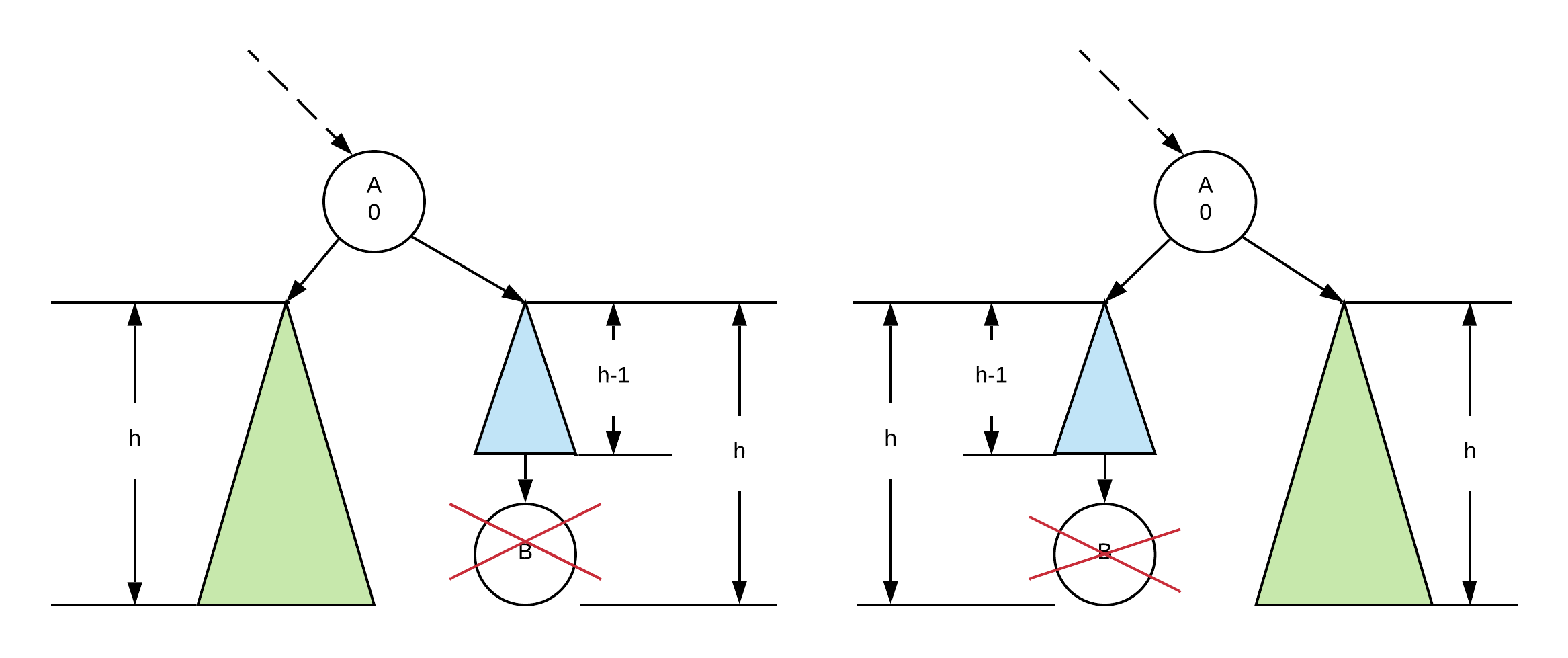
Let us consider the following. In each case, B is the node being removed, A is some node along the path to B

Balance of A was initially 0

Suppose that A initially had a balance of 0. Removing B, shortened the blue subtree. However, as the balance was 0 at A, A's balance will simply go either to +/- 1. No rotation needed. Also not only was no rotation needed, the height of the tree at A is actually exactly the same as it was before the deletion and thus, we can stop fixing the tree as nodes further up will not be affected

Balance of A was initially +/-1

Two things can occur. In the first case our node comes from the taller of the subtrees tree and it causes the tree to shorten.

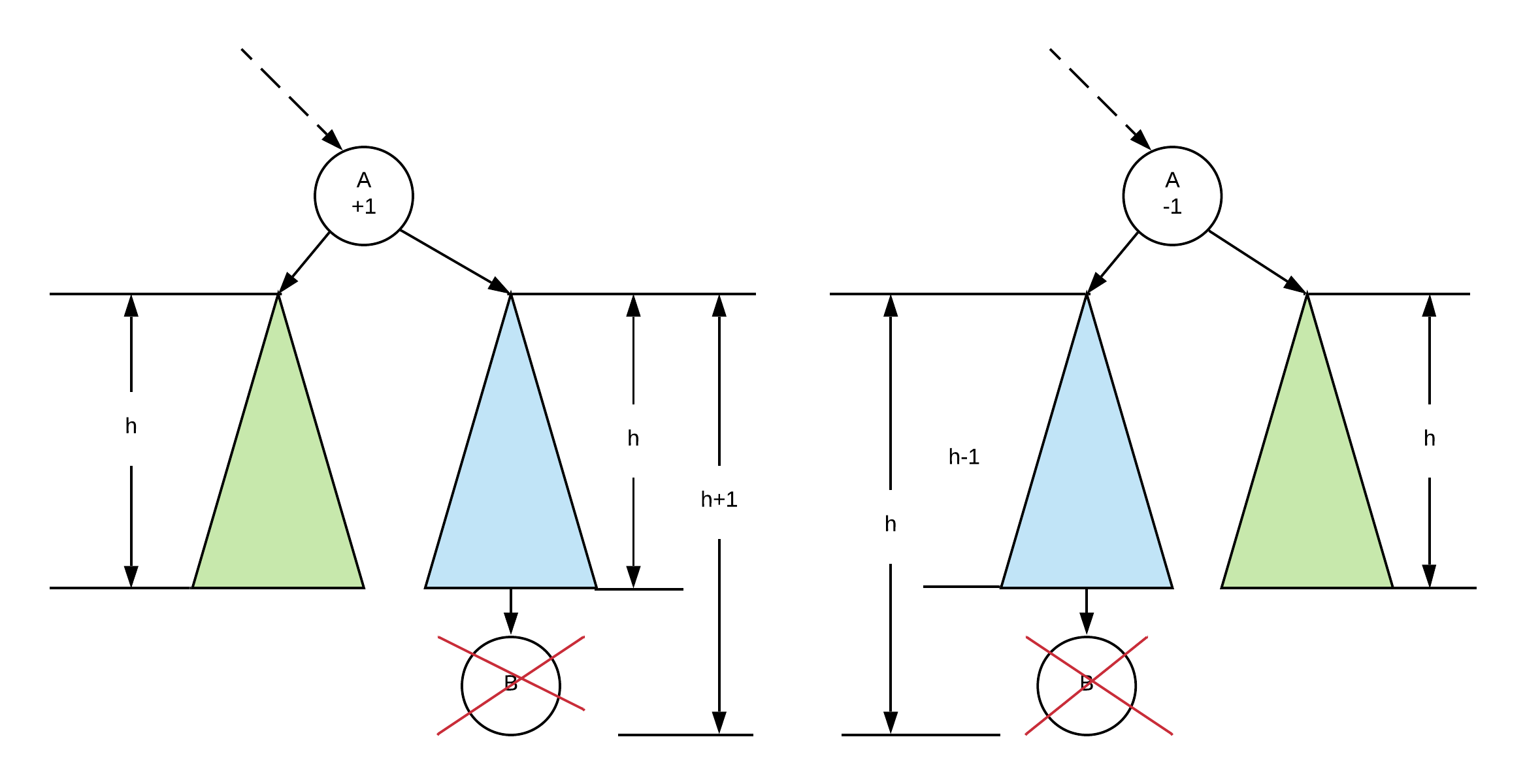
If that is the case then we do not have to do any rotations at A because A's balance will become 0. However, the subtree with root A did get shorter, so we must continue going up the tree as other nodes further up may require a rotation

The second case is when we take out a node from the shorter subtree:

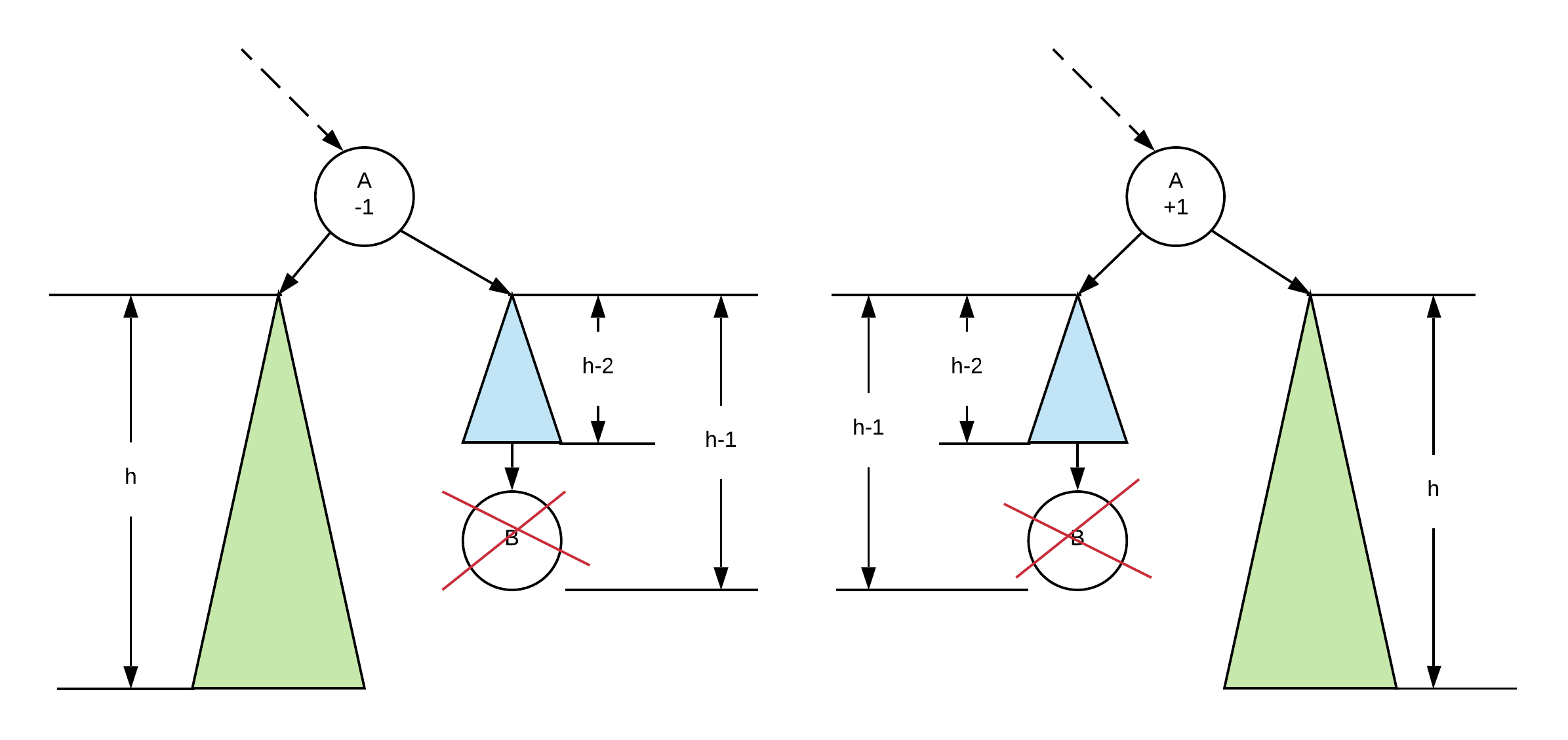
If we did this then our balance will go to +/- 2. This would require rebalancing. Like an insertion, rebalancing is simply a matter of applying a single or double rotation. We simply need to follow the same rules and perform the rotation

After a rebalancing a node the subtree might have become shorter than it was because of the rotation, and thus we may need to go further up the tree to fix it.