Skip to main content

Red Black Trees

Red-Black Trees are binary search trees that are named after the way the nodes are coloured.

Each node in a red-black tree is coloured either red or black. The height of a red black tree is at most 2 * log(n+1).

A red black tree must maintain the following colouring rules:

  1. every node must have a colour either red or black.
  2. The root node must be black
  3. If a node is red, its children must be black (note that this also implies that red nodes cannot have red parents)
  4. Every path from root to a null node must have exactly the same number of black nodes.
info

null nodes are also sometimes called null leafs. these are not really nodes.. they are the "nodes" that null pointers point to... so we when we think about counting black nodes we think about how many black nodes there are to every nullptr in the tree

Insertion​

We will begin our look at Red-Black trees with the bottom up insertion algorithm. This insertion algorithm is similar to that of the insertion algorithm we looked at for AVL trees/Binary search trees.

Insert the new node according to regular binary search tree insertion rules. Of the 4 colouring rules, the one rule we don't want to break is rule number 4. Everything we do is to avoid breaking rule 4 (every path from root to every null leaf has same number of black nodes). Thus, New nodes are added as red nodes. We then "fix" the tree if any of the rules are broken.

Note that because we inserted a red node to a proper red-black tree, the only 2 rules that might be broken are:

  1. rule 2: root must be black
  2. rule 3: red node must have black children

Rule 1 is pretty much not broken as we coloured it red. We also won't break rule 4 because we added a red node so the number of black nodes has not increased.

General Insertion Algorithm​

To insert into a red-black tree:

  1. find the correct empty tree (like bst) and insert new node as a red node.
  2. working way up the tree back to parent fix the tree so that the red-black tree rules are maintained.

Fixing nodes:​

  • If root becomes red, change it to black.
    • This won't break any rules because you are just adding 1 black node to every branch of the tree, the number of black nodes increase by 1 everywhere. This can only happen as the root as it is the only node that is part of every path from root to nullleaf
  • If there are two red nodes in a row:
    • Identify the following nodes:
      • upper red node as the Parent (P)
      • the lower red node as the Child (C)
      • parent of parent is Grandparent (G)
      • sibling of Parent as Parent's sibling (PS)
    • if the PS is black
      • perform a rotation (look at G->P->C, if they form a straight line do a zig-zig(single) rotation, if there is a bend, do a zig-zag (double rotation)
      • after rotation exchange G's colour with the node that took over G's spot. In otherwords
        • make which ever node (depends if it was zigzig or zigzag rotation... it will either be P or C) that took over G's node black
        • make G red
    • if the PS is red
      • exchange the colour of the grand parent with its two children. In otherwords
        • G becomes red
        • P and PS becomes black

Example​

Starting with an empty tree let us take a look at how red-black tree insertions work.

In the pictures below, null nodes (empty subtrees) are denoted as black circles

Insert 30​

All nodes are inserted as red nodes:

If the root is red, make it black:

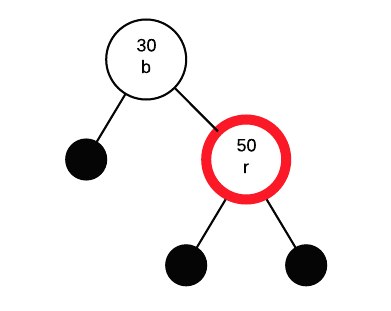
Insert 50​

Insert 50 as a red node, parent is black so we don't have to change anything

Insert 40​

Inserting 40 as a red node.

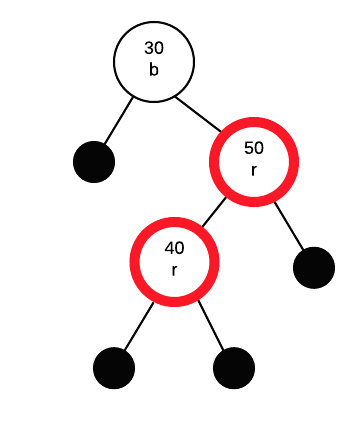
Two red nodes in a row. Identify G, P, PS and C

  • P - parent (upper red) - 50
  • C - child (lower red) - 40
  • G - grandparent 30
  • PS - parent's sibling - null node to left of 30

What we do depends on colour of PS. In this case PS is black, so we will be fixing this with a rotation

The type of rotation depends on the configuration of G, P and C. If the path is from G to C is straight (both left or both right) do a zigzig (single) rotation. If it is angled (left then right or right then left) we need to do a zigzag (double) rotation.

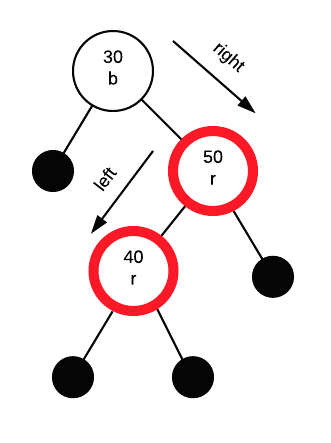
In this case, we need to do a zig zag (double) rotation.

Rotate first 40 and 50

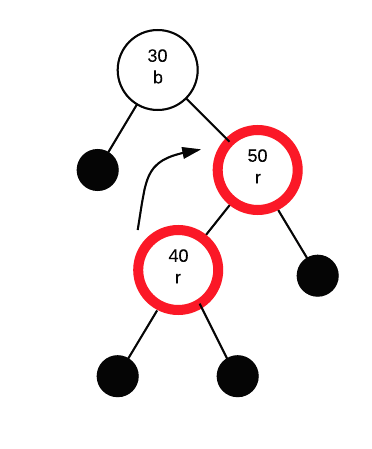
then rotate again with 30 and 40, this time doing a colour swap. A zigzag rotation is just an extra step that is needed to make the insertion path go in the same direction.

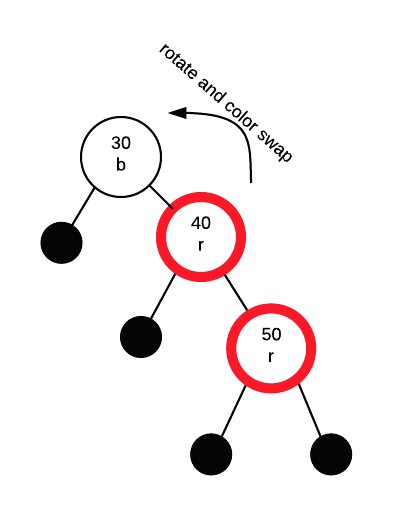
After rotations are complete, we exchange the colour between the node that took over G's spot (40 in this case) and G. Thus, 40 becomes black and 30 becomes red.

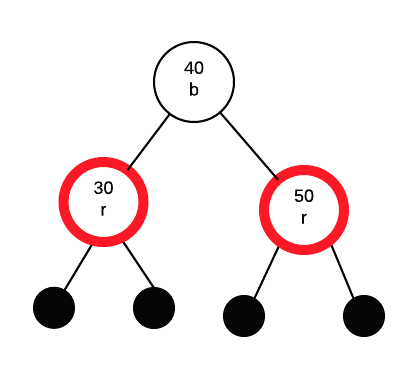
Insert 20​

inserting 20 as a red node.

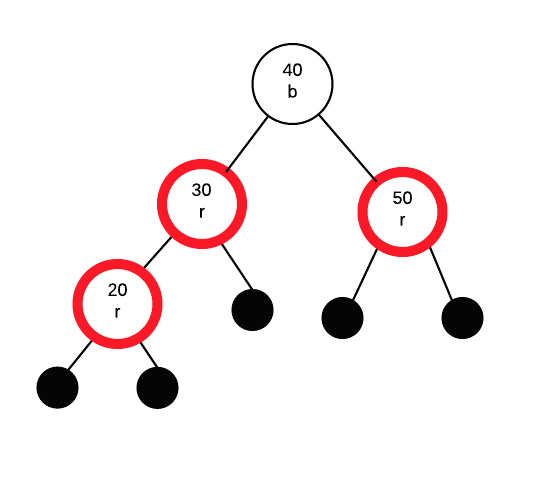
Two red nodes in a row. Identify G, P, PS and C

  • P - parent (upper red) - 30
  • C - child (lower red) - 20
  • G - grandparent - 40
  • PS - parent's sibling - 50

What we do depends on colour of PS. In this case PS is red. Thus we exchange colours between G and its two children:

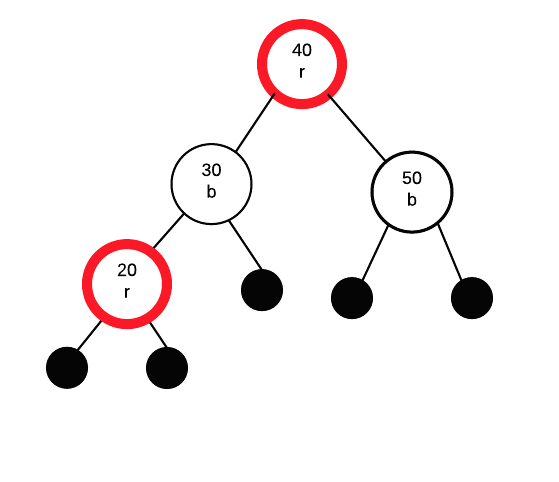
Doing so breaks rule 2: roots must be black. Thus, we need to fix that. As it is the root, we can just change it to black without causing other problems.

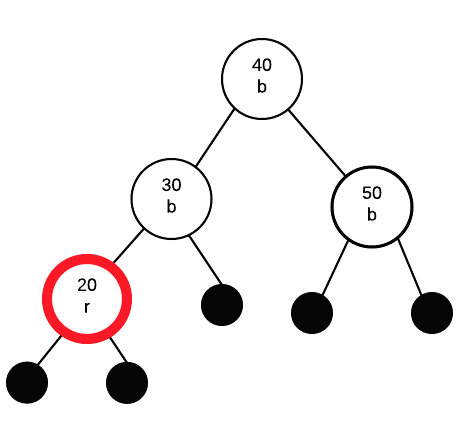
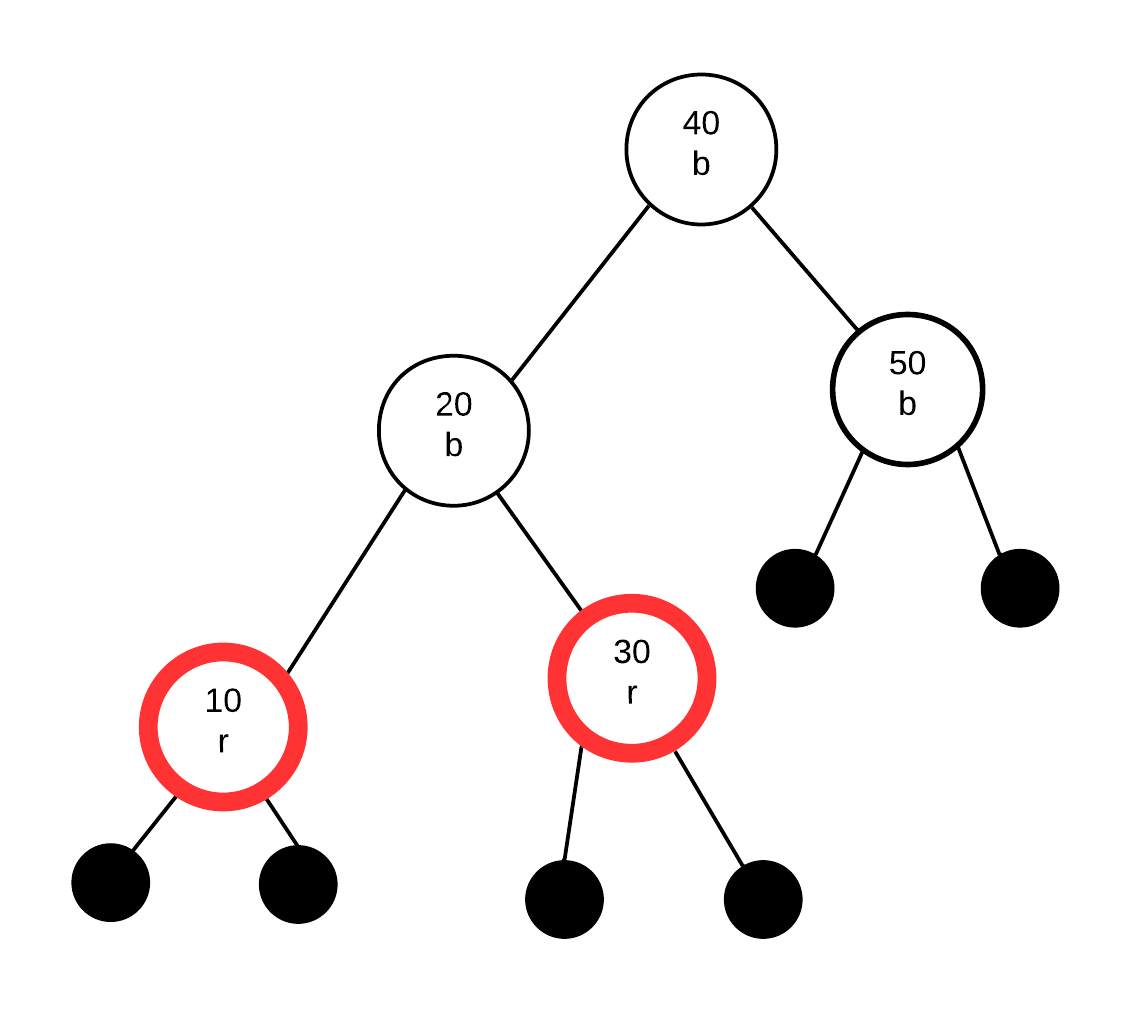
Insert 10​

inserting 10 as a red node.

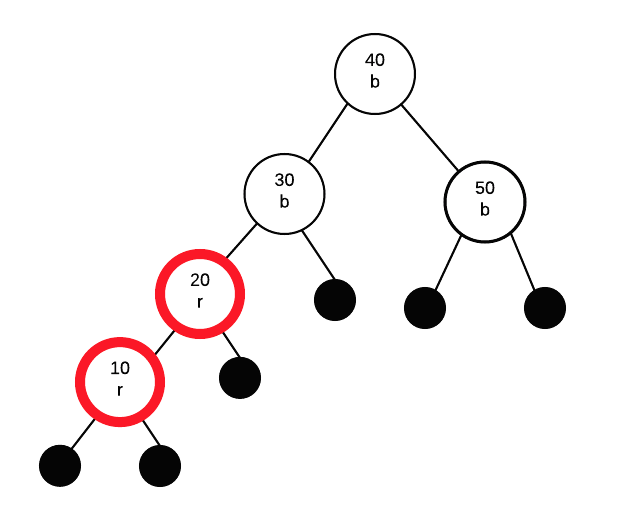
Two red nodes in a row. Identify G, P, PS and C

  • P - parent (upper red) -20
  • C - child (lower red) - 10
  • G - grandparent 30
  • PS - parent's sibling - null node to right of 30

What we do depends on colour of PS. In this case, the parent's sibling is black (null nodes are black). Thus, we will fix this with a rotation. Rotations are always done with G as the root of the rotation (the A in the rotation diagram)

This time, the path from G to P to C is "left" then "left". Thus, we only need to perform a single rotation, followed by swapping the colours of G and the node that took G's spot.

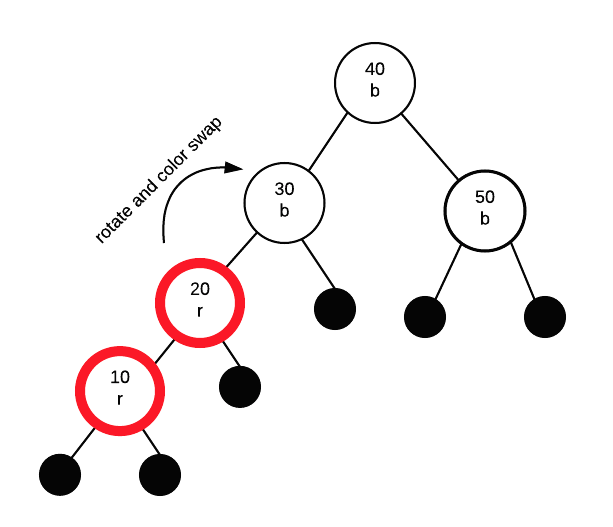
Finally we get: