Skip to main content

Tree Balance

Before we consider how to look make our tree behave properly, we should consider what it means for a tree to be "tree shaped". We want something a little more formal than just "tree shaped". In this section we look into these definitions:

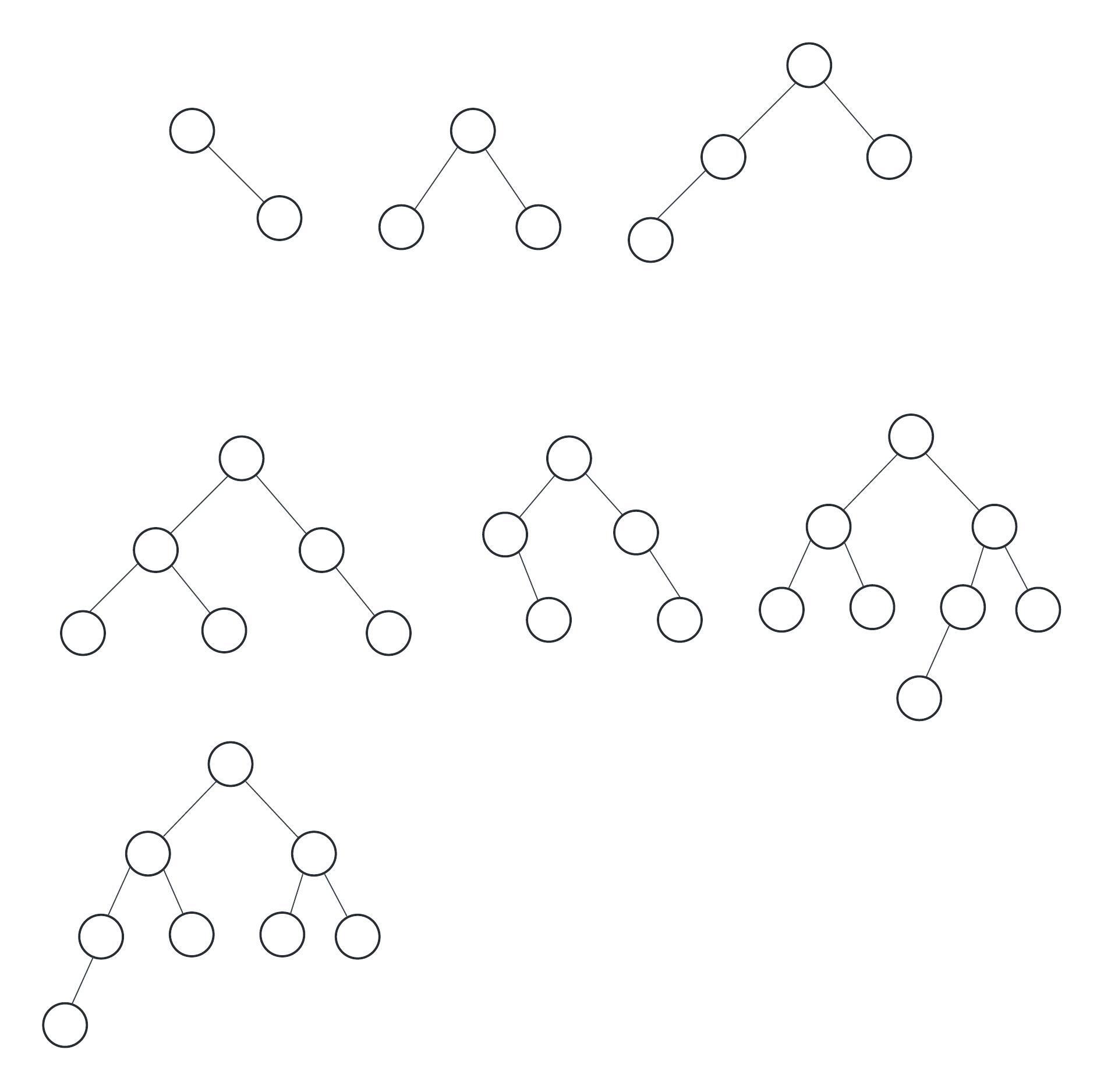
Perfectly Balanced Binary Trees​

A binary tree is perfectly balanced if for every node within the tree, the number of nodes in its right and left subtrees differ by no more than one.

Note how this definition says that this is true for every node... not just the root.

So if we take any subtree within a perfectly balanced tree, that subtree will be perfectly balanced.

Here are a few trees that are perfectly balanced.

perfectly balanced trees

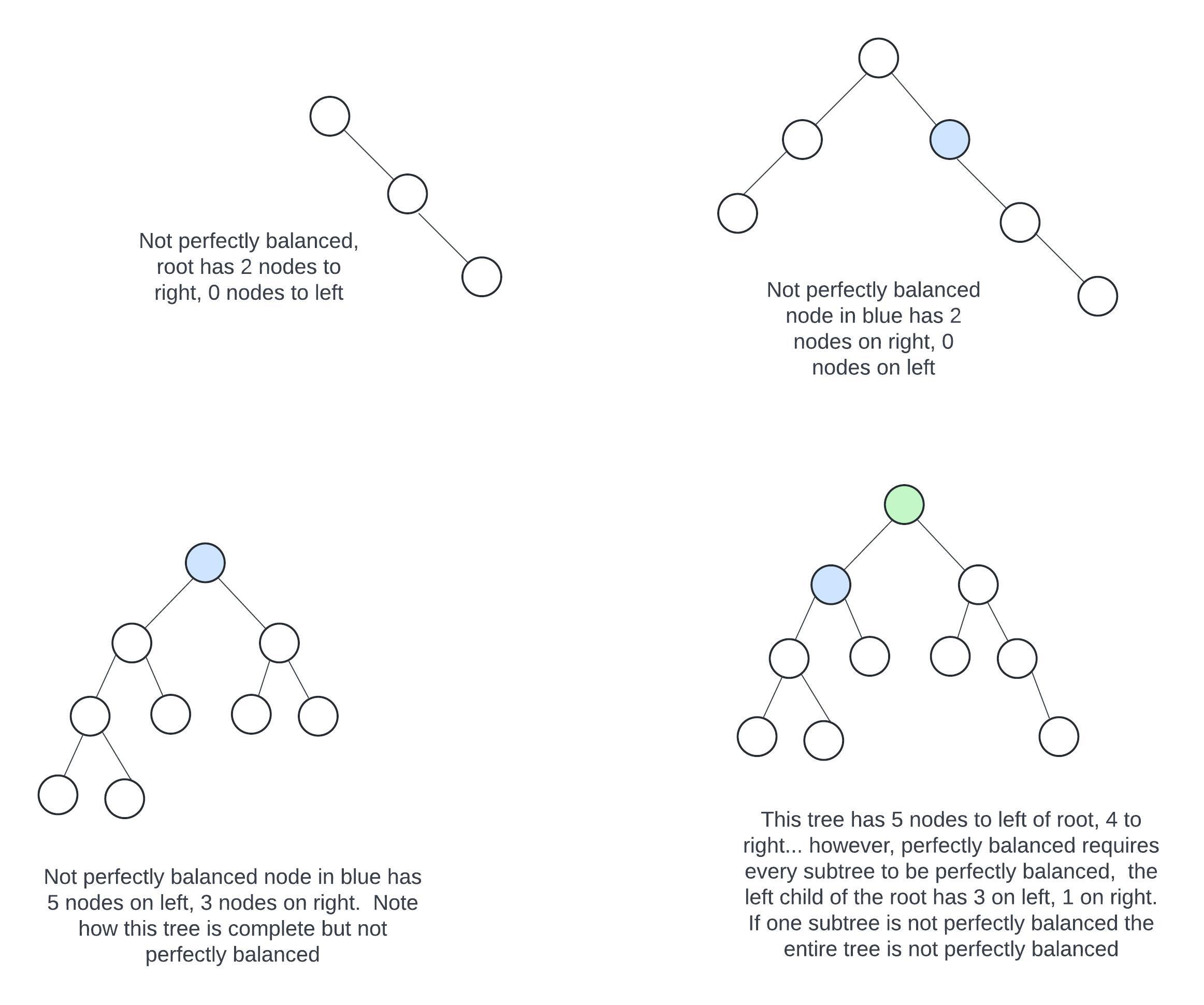
Here are a few that are not perfectly balanced and why they are not. not perfectly balanced trees

Notice that with this definition, a complete binary tree (which we said was a good tree) may not be pefectly balanced.

What this tells you is that the perfectly balanced tree description is too restrictive and will exclude many trees that actually have same performance as that of a perfectly balanced tree. Getting a tree to be perfectly balanced is also an expensive process. Thus, we typically will allow for a more relaxed definition of what a good "tree shape" is

Height Balanced Binary Trees​

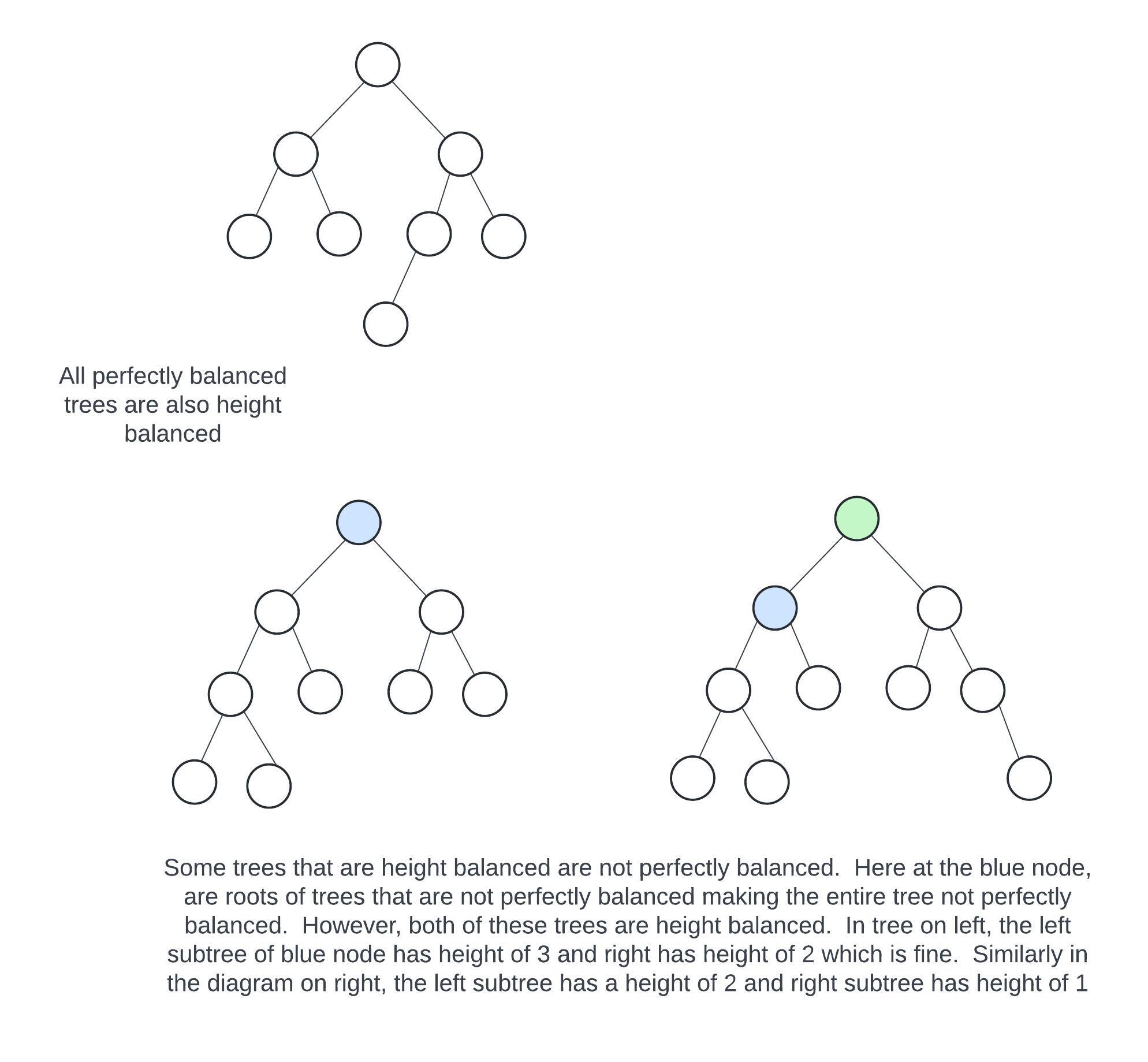
A binary tree is height balanced if for every node within the tree, the height of its right and left subtrees differ by no more than one.

Notice how this definition is almost the same as that of perfectly balanced trees. The only difference is that we measure the height of the tree as opposed to the number of nodes in the tree. This is useful as the height measures the maximum number of nodes we will consider.

Similar to perfectly balanced trees, the height balanced definition is recursively applied. Thus every subtree of a height balanced tree is also height balanced.

Here are some height balanced binary trees

height balanced trees

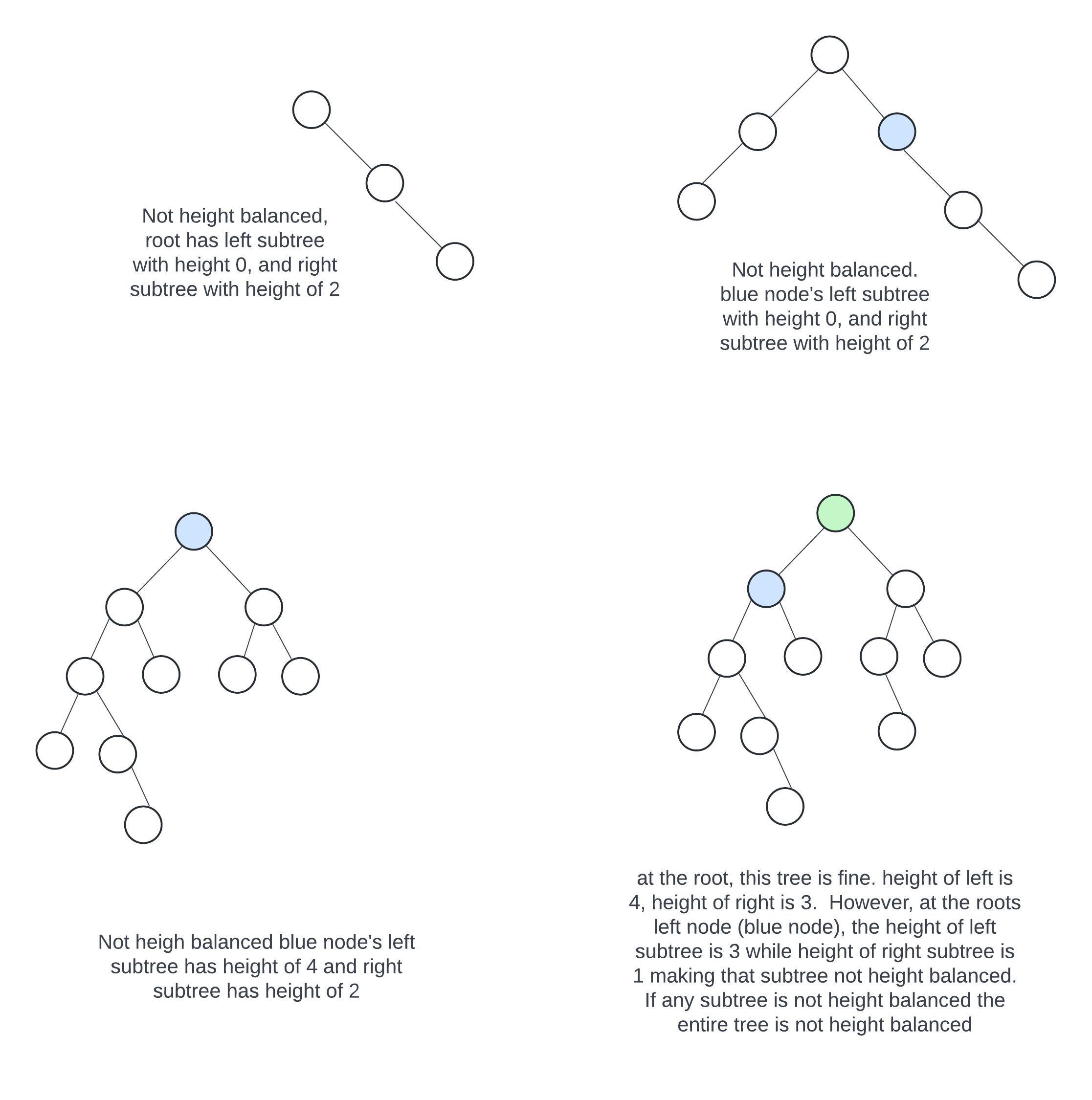
Here are some non-height balanced binary trees not height balanced trees

By ensuring that the trees on either side of a node are never significantly taller than each other, we can ensure that any operation done will never visit more nodes regardless of the value of the operand. This is how AVL trees work. By storing the height of a node's subtree in each node, a node balance can easily be calculated and used to maintain height balance

Branches​

A branch is defined as all the nodes from the root of the tree to a leaf inclusive of both root and leaf. Another way of looking at whether a tree is "tree shaped" is to consider the differences between the length of the the branches. We can look at whether or not a tree is good by looking at the differences in the length of the branches. This is how red-black trees work. They use a set of node colouring rules to ensure that no branch is more than twice the length of any other branch in the tree.